引言
扩散磁共振成像(Diffusion Magnetic Resonance Imaging,dMRI)是一种先进的非侵入性成像技术,通过检测生物组织中水分子的微观运动(即扩散)来揭示组织的微结构和连接性信息.在生物组织中,由于细胞膜、细胞排列以及大分子等结构的影响,水分子的扩散可能呈现各向同性或各向异性的特性.扩散张量成像(Diffusion Tensor Imaging,DTI)是最早被提出通过拟合扩散张量模型来估计纤维方向分布(Fiber Orientation Distributions,FOD)的dMRI模型.当扩散表现出足够程度的各向异性时,大脑纤维主要方向可以计算并进行追踪,最终可获得该结构的三维重建结果,例如脑白质(White Matter,WM)的纤维束成像[1].然而,DTI模型在处理具有复杂微结构和受限扩散的组织区域时存在一定局限性[2,3].约束球面反卷积(Constrained Spherical Deconvolution,CSD)[4]是一种基于球面谱的dMRI数据分析方法,旨在从复杂的扩散信号中提取出更准确的纤维束信息,可以有效的重建复杂的纤维束.CSD在扩散成像领域得到了广泛的应用,尤其是在WM区域的纤维束成像方面.然而,在灰质(Gray Matter,GM)区域的纤维束成像中,由于神经元的结构复杂,传统的CSD模型不能很好的用于灰质微结构成像参数的估计.
单壳CSD方法的dMRI数据通常在b值为3 000 s/mm2、梯度方向数为60的条件下进行采集[5].采用较高b值的dMRI成像数据可提高对神经纤维的角度分辨率,但同时也会降低图像信噪比(Signal to Noise Ration,SNR),导致结果偏差.因此,在实际应用中需要权衡采集数据的b值,以获得最优结果.随着磁共振成像设备升级,数据采集时间缩短,使得多b值dMRI数据采集成为可能[6,7],可进一步提高纤维方向估计的稳定性.Jeurissen等人[8,9]在CSD的基础上提出了多组织CSD方法,通过考虑部分容积效应,进一步提高了在WM中纤维方向估计的准确性.在目前的方法中,通常将WM假设为各向异性,GM假设为各向同性.然而,GM中存在多种尺度的神经元胞体和树突,这些结构的存在导致水分子在GM中的扩散也会在某种程度上受到限制,因此如果将GM的扩散特性完全视为各向同性扩散,可能会降低大脑FOD估计的准确性.忽略GM的各向异性在dMRI应用中可能导致对大脑微观结构和功能的理解不准确,而考虑GM的各向异性可以提供更精确的细胞形态学描述,包括轴突和树突的分布和取向,从而更好地理解大脑结构复杂性以及理解大脑的连接性和功能,揭示大脑发育过程中的动态变化,并通过捕捉GM中的细微形态变化,更早地识别神经发育障碍和其他神经系统疾病,从而提高诊断准确性[10,11].生物物理模型从另一个角度展开了微结构成像的研究,这些模型考虑了大脑的不同组织特性,将大脑组织分为多个隔室.球棍模型最早被提出,在其基础上又通过考虑扩散分布的不同提出了复合受阻受限扩散模型(Composite Hindered and Restricted Model of Diffusion,CHARMED)[12].Zhang等人[13]提出的神经突定向弥散和密度成像(Neurite Orientation Dispersion And Density Imaging,NODDI)模型是一种微观结构模型,该模型由神经胶质细胞、轴突和细胞外空间的三个隔室组成,可以通过临床上的成像方法来量化GM与WM的微观结构变化.Palombo等人[14]在多隔室模型的基础上提出了体细胞和神经突密度成像(Soma And Neurite Density Imaging,SANDI)模型,将多隔室模型应用于GM中,该模型将细胞体大小和密度与轴突密度相结合,从而能够进行GM微结构成像[15].SANDI将细胞内空间分为胞体和神经突,进一步分析大脑微结构.由于SANDI明确了胞体对细胞内信号的贡献,因此可以获得GM部分的信号,从而能够提取GM部分的各向异性.
本文针对GM低各向异性特性,提出了一种基于SANDI的GM多壳CSD算法(GM Multi-Shell Constrained Spherical Deconvolution,GM-MSCSD),该方法考虑到WM和GM中扩散特性的差异,通过重建GM中的各向异性扩散信号来改进FOD估计.首先,使用两种仿真方法对真实神经元的胞体部分数据进行了dMRI信号仿真,以验证GM部分的扩散特性.然后,利用真实的大脑数据进行实验.通过选择不同的大脑区域,对传统CSD方法和GM-MSCSD算法估计的纤维方向进行对比分析,以评估GM-MSCSD方法在GM区域的效果.最后,对实验结果进行讨论与分析.总的来说,本文提出的GM-MSCSD算法改进了传统的CSD方法,结合SANDI模型能够精确估计胞体密度和大小的特点,从而将WM微结构成像推广至GM微结构成像,在估计GM区域的神经纤维走向方面具有更高的准确性,在GM的纤维方向估计方面具有一定的优势.
1 方法理论
1.1 SANDI模型
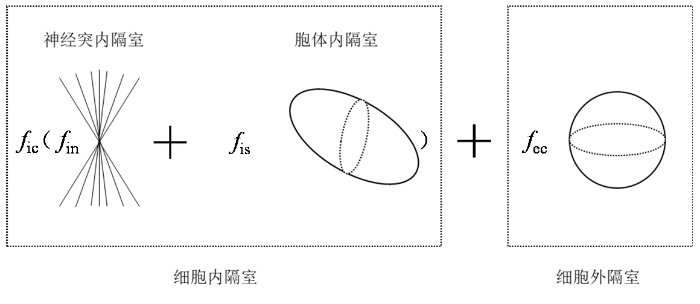
SANDI是由Palombo等人提出的一种扩展多隔室模型的方法.该模型首次结合了体细胞的大小和密度,利用dMRI和基于模型的方法,以非侵入性的方式估计GM微结构[15].该模型提出将胞体视为细胞内信号的一个组成部分,引入了一个三隔室模型假设,用于分离和量化胞体三隔室模型,将细胞分为神经突内隔室和胞体内隔室以及细胞外隔室三部分,总细胞信号由这三个隔室的信号组成,归一化总信号为:
其中b表示梯度感因子,S(b)为对应b值采集的总信号,S0(b)为未施加梯度方向采集所得信号,细胞内和细胞外的总相对信号分数fic、fec满足fic+fec=1,神经突和胞体的相对信号分数fin、fis满足fin+fis=1.Ain、Ais和Aec分别是神经突和胞体内扩散受限的归一化信号以及细胞外空间的归一化信号.(1)式提供一个更为通用的模型,该模型考虑了神经组织微结构中的胞体成分.按照之前的研究[16⇓-18],将大脑分为了细胞内和细胞外两个隔室,这两个隔室通过相对信号分数fic和fec对总细胞内信号做出贡献,这些信号分数相加等于1,如图1所示.因此,fic、fec、fin和fis并不是dMRI体素中相应组织成分的体积分数,而是相应组织隔室的相对dMRI信号分数.
图1
Ais是胞体所贡献的信号部分,被假设源自于一组受限于半径为rs的球体内的扩散的水分子.通过使用蒙特卡洛扩散在实际神经元模型中仿真,实验结果表明,在典型的胞体大小和体积分数下,神经突内和胞体内扩散水分子之间的交换是可以忽略不计的[19],因此可以假设在神经突内的水分子扩散与胞体内的水分子扩散之间的交换可忽略.
由于大脑GM部分主要由胞体和树突组成,因此主要关注的是胞体内隔室,其归一化信号形式如(2)式所示:
其中Dis是水的扩散系数,δ和Δ是扩散梯度脉冲宽度和间隔,g是扩散梯度脉冲的幅度,am是球贝塞尔函数递推方程
通过(1)式以及(2)式得到胞体部分的信号表达式:
1.2 多壳CSD模型
在CSD中,在每个像素位置上的测量信号S可以用纤维方向分布F(θ,ϕ)与响应函数K(θ)的在积分球域S2上卷积表示,如(4)式所示,其中,响应函数K是根据数据估算的.
多壳CSD模型通过融合多个b值的信息来增强对复杂扩散信号的建模能力.在该模型中,每个b值代表了一组不同梯度强度的扩散梯度方向,从而使得模型能够捕捉到更加丰富的扩散信号信息.
为适应多b值的dMRI数据,在传统CSD方法基础上,通过增加响应函数矩阵的行数来扩展矩阵的大小,如(5)式所示,其中n代表了b值的数量.
虽然多壳CSD可以在含有纯WM的体素中提供高质量的FOD估计,但在包含其他组织类型如GM和脑脊液(Cerebrospinal Fluid,CSF)的体素中,单一纤维响应函数可能不再适用.因此,结合WM、GM和CSF三种组织提出了多组织CSD方法[8].
在传统的多组织CSD研究中,引进了一种damped Richardson-Lucy(dRL)[20]的多壳球谐反卷积算法来解释多组织类型,包括WM、GM和CSF,如(6)式所示:
其中S是收集的n个扩散加权信号,S0是非扩散加权信号,K矩阵分别表示与WM、GM和CSF所对应的响应函数矩阵,f是所对应的信号分数,FODWM是与WM相关的纤维取向分布,GM和CSF都被认为是各向同性.
1.3 改进CSD模型的GM微结构成像方法
本文采用了改进的CSD方法,并结合dRL算法对模型进行求解,以获取GM相关的纤维取向分布.首先,通过SANDI模型获得GM部分信号以及与之对应的响应函数矩阵.随后,使用本文提出的GM-MSCSD算法,对提取出的GM信号进行分析,估计GM区域的纤维取向分布.
在(6)式只是针对WM部分的各向异性部分进行建模,将GM完全认为是各向同性的,但这与事实上的不符,因为GM部分存在的胞体和树突,水分子在GM部分的扩散是各向异性扩散的.针对上述问题,对(6)式进行了重新设计,允许任意数量的独立各向异性组织进行反卷积以估计所对应的FOD[21],改进的公式如(7)式所示:
其中SGM是收集的GM部分扩散加权信号,SGM0是GM部分非扩散加权信号,二者由SANDI模型生成.K矩阵表示与GM所对应的响应函数矩阵,其由SANDI模型生成.
其中,FOD(k)是在单位球体上沿着第
其中正则项u(k)根据当前计算所得的FOD的幅值和扩散加权信号的标准差在迭代时进行更新,如(10)、(11)式所示:
其中,r表示一个n×1的向量,用于调节每个FOD中元素的阻尼水平;v是描述阻尼曲线轮廓以及阻尼开启和关闭速度的几何参数.v值越小,r从0到1的过程会变得更加平缓,过渡区域越宽.这个参数用于将阻尼曲线的尺度与重建的FOD轮廓的幅度匹配.如果曲线过宽,阻尼可能会影响到高幅度的分量,而对较小的分量影响则不够明显.因此需要设置一个合适的参数来匹配以达到平衡.根据实验结果,常数v被设置为8,η被设置为当前FOD最大系数(即各方向上的幅度值)的两倍[20].max表示取最大值函数,std表示标准差.
综上,由(12)式可以获得GM部分估计的纤维方向.
2 实验结果与分析
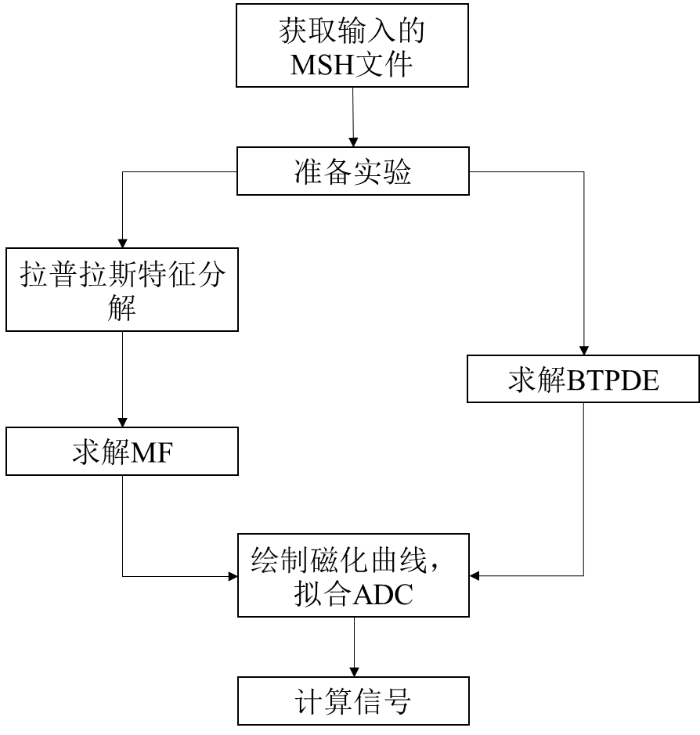
为了验证提出的GM-MSCSD方法的有效性,本文选择算法开发及数值计算软件Matlab R2022b作为平台,首先使用真实神经元进行dMRI仿真,获得神经元的模拟dMRI信号;然后利用真实的大脑数据进行实验,选取不同的大脑区域,将传统的CSD方法与本文算法重建的纤维方向对比分析.
2.1 仿真实验
在dMRI中,通过应用时变磁场梯度以对水分子扩散进行编码.在旋转坐标系中,水中质子的横向磁化强度满足BTPDE[24]:
其中,γ = 2.67513×108rad·s-1·T-1是水质子的旋磁比,I是虚数部分,σ是神经元的三维几何域Ω的固有扩散系数,磁化强度M是位置x和时间t的函数,M的值取决于扩散梯度向量g和时间分布f(t).有效时间分布f(t)描述了扩散编码磁场梯度的影响,并且向量g包含磁场梯度的幅值和方向信息.
基于矩阵形式(Matrix Formalism,MF)的BTPDE解表示建立在给定几何配置的广义拉普拉斯特征函数上.这些是广义拉普拉斯算子− ▽·σ▽的特征函数,其边界和界面条件也满足BTPDE,该方法不依赖于梯度序列.矩阵形式通过设定最小长度尺度来截断拉普拉斯特征模的数量,使其维持在一个可接受的水平上.因此,与梯度序列相关的Bloch-Torrey算子可以在截断的拉普拉斯特征函数基础来表示.这种方法允许使用简单的解析表达式近似求解任意长度尺度的BTPDE.
本文拟设定的是脉冲梯度自旋回波(Pulsed-Gradient Spin Echo,PGSE)序列[26],具有两个持续时间为δ的矩形脉冲,间隔时间为Δ−δ,其轮廓f(t)为:
其中
在dMRI中,b值是用来量化扩散加权信号的参数,它与水分子在生物组织中的扩散受限情况有关.b值通常与扩散编码梯度向量g、持续时间δ和两个梯度脉冲之间的时间间隔Δ有关:
本实验使用NeuroMorpho数据库(www.NeuroMorpho.org)提供的纺锤体神经元03b_spindle4aACC作为仿真对象,其详细参数见表1. 纺锤体神经元细胞是一种具有独特纺锤形胞体的神经元,纺锤顶部延伸出一个轴突,并且在相对方向仅有一个轴突,如图2所示.尽管GM中存在多种类型的神经元,它们在胞体结构和扩散特性上与纺锤体神经元存在一定的相似性,特别是树突和轴突结构,因此选择纺锤体神经元作为代表神经元细胞进行仿真实验以说明其扩散异性.纺锤体神经元细胞包含了胞体和两个轴突分支,但考虑到研究的焦点是GM组织,即神经元的细胞体部分,因此利用神经形态学的空间信息对神经元进行了精细的分割和提取.NeuroMorpho数据库提供了神经元细胞的SWC格式文件,扩散信号仿真前需要将SWC格式文件处理转换为MSH格式的体四面体网格.文献[25]将NeuroMorpho数据库中部分神经元的SWC格式文件转换为MSH格式,且对完整神经元进行了分割,得到了对应的胞体与轴突MSH格式文件.本文从
表1 纺锤体神经元细胞参数
Table 1
| 神经元ID | 有限元节点数 | 脑区 | 平均直径/µm | 总高度/µm | 胞体体积/µm3 | 总体积/µm3 |
|---|---|---|---|---|---|---|
| 03b_spindle4aACC | 17370 | 前扣带 | 1.43 | 336.33 | 3098.39 | 4070.19 |
图2
图2
纺锤体神经元03b_spindle4aFI的三个部分:胞体和两个轴突分支
Fig. 2
Three parts of spindle neuron 03b_spindle4aFI: soma and two axon branches
图3
图4
图4
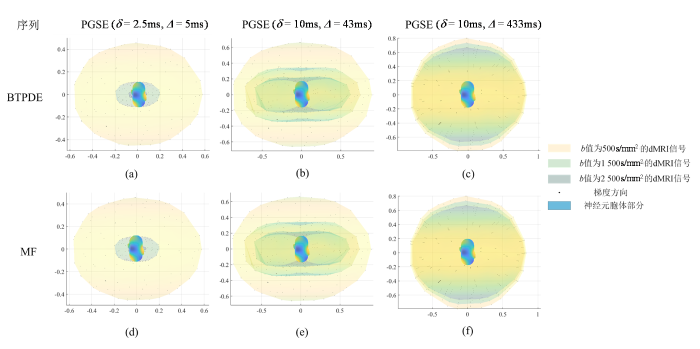
使用BTPDE和MF方法仿真的纺锤体神经元的胞体归一化dMRI信号.(a)、(d)对应PGSE(δ=2.5 ms,Δ=5 ms)时不同b值生成的信号;(b)、(e)对应PGSE(δ=10 ms,Δ=43 ms)时不同b值生成的信号;(c)、(f)对应PGSE(δ=10 ms,Δ=433 ms)时不同b值生成的信号. 图中横纵坐标代表了归一化信号的大小|S/S0|;图中最外圈信号值对应的b值为500 s/mm2,中间对应的b值为1 500 s/mm2,最内圈对应的b值为2 500 s/mm2.
Fig. 4
dMRI signals of spindle neuron soma simulated using BTPDE and MF methods. (a) and (d) correspond to signals generated at different b values at PGSE (δ=2.5 ms, Δ=5 ms); (b) and (e) correspond to signals generated at different b values at PGSE (δ=10 ms, Δ=43 ms); (c) and (f) correspond to signals generated at different b values at PGSE (δ=10 ms, Δ=433 ms). The horizontal and vertical coordinates of the figure represent the normalized magnitude of the signals |S/S0|; the signal value in the outermost circle of the figure corresponds to a b value of 500 s/mm2, the one in the middle corresponds to a b value of 1 500 s/mm2, and the one in the innermost circle corresponds to a b value of 2 500 s/mm2.
图5
图5
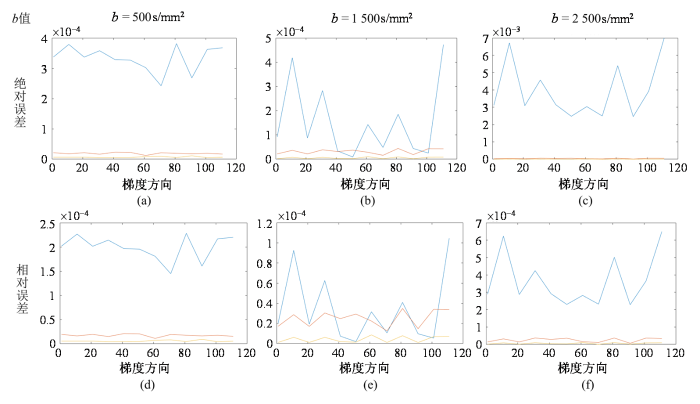
使用BTPDE和MF方法仿真的dMRI信号之间的绝对误差和相对误差.(a)、(b)和(c)分别展示了在b值为500、1 500和2 500 s/mm2时,不同扩散时间下的绝对误差;(d)、(e)和(f)则对应展示了相同b值条件下的相对误差. 图中蓝线为(δ=2.5 ms,Δ=5 ms)时的误差,红线为(δ=10 ms,Δ=43 ms)时的误差,黄线为(δ=10 ms,Δ=433 ms)时的误差;图中纵轴表示误差的大小,横轴代表梯度方向;115个梯度方向均匀分布在整个球面上
Fig. 5
Absolute and relative errors between dMRI signals simulated using BTPDE and MF methods. (a), (b), and (c) show the absolute errors at different diffusion times for b values of 500, 1 500, and 2 500 s/mm2; (d), (e), and (f) correspondingly show the relative errors for the same b value condition. The blue line of the figure is the error at (δ=2.5 ms, Δ=5 ms), the red line is the error at (δ=10 ms, Δ=43 ms), and the yellow line is the error at (δ=10 ms, Δ=433 ms). The vertical axis of the figure represents the magnitude of the error, the horizontal axis represents the gradient directions;115 gradient directions uniformly distributed over the entire sphere
在dMRI中,b值作为一个核心参数,直接关联着水分子在生物组织内扩散受限的量化.当实验中设定相同的b值时,调整δ和Δ时,g的幅度也相应地改变,从而保持b值恒定.图4显示在同一列结果中,保持δ和Δ不变,改变b值,g的幅度也随之改变,其信号也相应地改变.在实现这一过程中,仅需固定δ和Δ的值,通过改变b值来探索其对信号差异性的影响.b值作为dMRI中的关键参数,其大小受到g、δ和Δ的共同调控.通过控制这些参数能够实现对水分子扩散受限程度的量化,其差异如图5所示,通过分析不同梯度方向、不同Δ和不同b值下两种仿真方法仿真获得的加权复合信号之间的信号差,反映在相同条件下,两个模型对信号计算结果的偏差程度.图5第一行图展示了BTPDE信号和MF信号之间的绝对误差,并将结果标准化为初始信号的强度.这一分析旨在研究BTPDE和MF信号相对于初始信号的变化情况.第二行图显示了BTPDE信号和MF信号之间的相对误差,通过计算两个信号之间的差异,然后将结果除以同一位置上BTPDE信号的最大值来获得相对误差.
从图5中可以观察到,由于115个梯度方向均匀分布在整个球体上,BTPDE和MF之间的信号差异随梯度方向的变化而变化,呈现出梯度方向依赖性,并且在不同的Δ和b值下,误差表现出不同的特点.当b值为1 500 s/mm2时,Δ对两者之间的信号误差影响较小;而当b值为500 s/mm2和2 500 s/mm2时,误差较大.值得注意的是,对于相同的扩散时间,信号的相对误差首先随着b值的增加而减小,然后再增大.在相同的扩散时间下b值为1 500和2 500s/mm2的信号误差随着梯度方向先减小后增大.这些观察结果有助于更全面地理解两种仿真方法在不同条件下生成信号的特点和差异.
通过以上两种仿真方法可以获得单个神经元胞体的dMRI信号,观察到其信号在不同梯度方向的扩散不同.由于胞体形态的非规则性及其直径的差异性,因此直径的变化直接对胞体在各个方向上的扩散信号产生了显著影响.这一结果证实了神经元胞体部分即其对应的GM组织中也存在方向性特征,从而进一步说明了对GM区域的纤维方向估计是可行的.通过两种仿真方法的对比分析,可以得出使用MF这种近似方法能快速便捷地仿真神经元扩散信号,并通过改变b值等参数以观察分析信号的改变,以此可以更好地了解大脑微结构.综上,本实验成功验证了神经元胞体在dMRI中的方向性扩散特性,还验证了MF近似方法作为研究大脑微结构的有效性.
2.2 真实大脑数据实验
本实验所使用的真实大脑数据来自扩散图像(Diffusion Image in Python,DIPY)数据库公开的功能整合神经科学中心的医学图像(Center of Functionally Integrative Neuroscience,CFIN)数据集,该数据集可在以下网址获得:
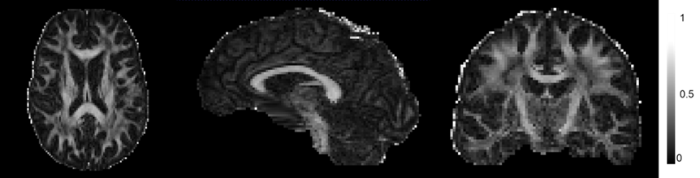
采用DTI技术对真实大脑数据进行了深入的分析.通过DTI技术获取了大脑WM和GM的各向异性分数(Fractional Anisotropy,FA).这一参数是评估水分子在大脑中扩散运动各向异性程度的关键指标,其值介于0到1之间,能够反映出组织的物理特性和微观结构.具体而言,FA值的高低直接反映了水分子扩散运动的方向性.FA值越高,表明水分子的扩散运动更具有方向性,即各向异性更强.如图6所示,WM区域的FA值普遍高于GM区域,这一发现与已知的大脑解剖结构相吻合,数据显示,GM的FA值普遍低于0.2,而WM的FA值则普遍高于0.3.表2列出了WM和GM的FA平均值,通过对比WM和GM的FA平均值可以进一步证实WM具有较高的各向异性,而GM的各向异性则相对较低,但GM并非完全各向同性,其内部也存在一定程度的各向异性特性.
图6
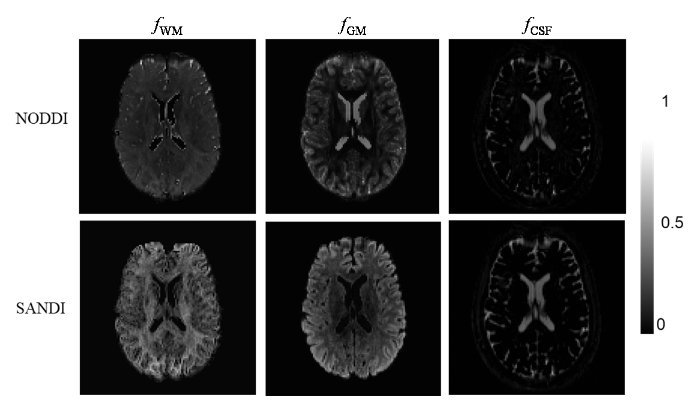
本实验采用基于NODDI和SANDI生物物理模型生成各个组织的信号分数并获得输入的GM信号,并将这两个模型分别构建的GM响应函数矩阵应用于CSD方法中对GM区域的纤维方向进行估计.在本研究中,使用AMICO工具包来获取两种模型(NODDI和SANDI)相关组织的信号分数[27].两种方法估计的大脑组织信号分数如图7所示,每一列显示了生成的WM信号分数图fWM、GM信号分数图fGM和CSF信号分数图fCSF,每一行分别展示了NODDI和SANDI两种方法的估计结果.两种方法都能够将大脑分为三种组织,与真实的人脑解剖结构相符合.这两种方法都能够获得GM部分的信号分数,因此可以通过获得的信号分数来获取GM部分的dMRI信号,从而进行GM部分的纤维方向估计.结合1.3节中导出的成像参数,验证其对微观结构成像的敏感性,并与SANDI相似参数进行比较.
图7
表3 大脑组织信号分数平均值
Table 3
| 模型 | 组织 | fWM | fGM | fCSF |
|---|---|---|---|---|
| NODDI | WM | 0.70 | 0.19 | 0.11 |
| GM | 0.38 | 0.56 | 0.06 | |
| CSF | 0.00 | 0.00 | 1.00 | |
| SANDI | WM | 0.65 | 0.35 | 0.00 |
| GM | 0.20 | 0.77 | 0.03 | |
| CSF | 0.06 | 0.04 | 0.90 |
图8
图8
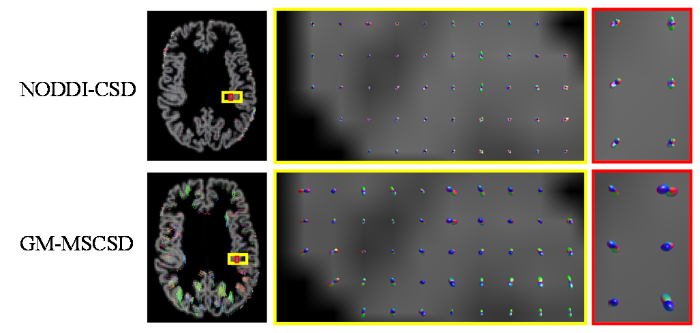
NODDI-CSD方法和GM-MSCSD方法的脑GM内部纤维重建结果
Fig. 8
Fiber reconstruction results within brain GM by NODDI-CSD method and GM-MSCSD method
图9
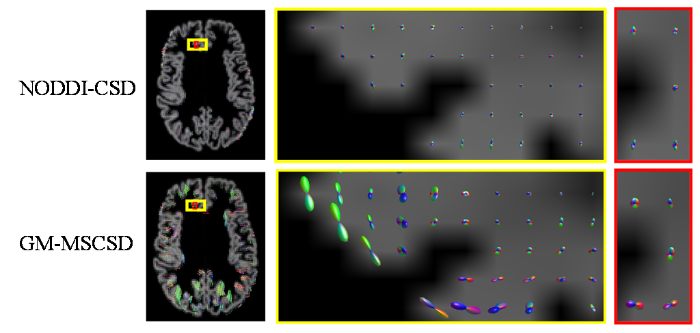
图9
NODDI-CSD方法和GM-MSCSD方法的脑GM与WM过渡处纤维重建结果
Fig. 9
Fiber reconstruction results at the transition between brain GM and brain WM by NODDI-CSD method and GM-MSCSD method
通过图8、图9可以观察到,使用GM-MSCSD方法估计的GM纤维方向与NODDI-CSD方法相似.在大脑皮层内部,即GM区域,神经细胞胞体众多而轴突相对较少,由于胞体排列的随机性,胞体对纤维整体方向的影响是微弱的,但这影响不能忽视.因此,在GM内部的纤维方向虽然呈现出轻微的各向同性倾向,但仍然存在一些显著的方向性.这些方向性可能是由于神经细胞体的排列方式、局部组织结构的微观特征以及细胞间相互作用等因素所导致的.因此,在GM内部,纤维方向并不像在WM中那样明确,但仍然存在一些可辨识的取向特征.当处于GM与WM的交界处时,由于受到WM和浅表白质部分的影响,GM区域的纤维方向表现出更加显著的定向性.这是因为在这一区域,GM的微观结构与邻近的WM部分相互影响,使得纤维方向更加明确和可识别.
根据图9的展示结果,可以观察到使用GM-MSCSD方法获得的脑GM纤维方向,在大多数GM体素中都呈现出解剖学上可信的峰值.这些峰值所代表的纤维方向与深WM区域的纤维束大多呈垂直关系.根据先前的研究[15],NODDI在GM中对于神经突密度指数(Neurite Density Index,NDI)等部分指标的估计不够可靠,这表明NODDI更适用于获取WM中的微结构特征.相比之下,GM-MSCSD方法结合SANDI模型,更准确地考虑了胞体在信号形成过程中的影响,因此对于大脑GM部分纤维的估计更加符合实际情况,具有更高的可行性和准确性.这一结果进一步验证了GM-MSCSD方法在解析GM纤维方向方面的有效性.
3 结论
基于GM的扩散特性,传统的CSD方法通常将其假设为各向同性扩散.但是,这种方法往往无法提供更加详细的GM信息.在本文中,针对传统方法在GM微结构成像中的局限性,提出了基于SANDI的GM-MSCSD方法.该方法充分考虑了GM的组织成分对扩散特性的影响,实现了对GM微结构更精确的成像分析.首先,通过仿真实验成功模拟了胞体组织的扩散信号,证明了GM中存在各向异性扩散特性,从而验证了使用GM-MSCSD方法对GM区域纤维方向进行估计的可行性.这一发现克服了传统观念中GM被视为各向同性扩散的局限,为深入理解GM的微观结构提供了新的视角.随后,利用公开数据库的真实人脑数据进行了实验验证.GM-MSCSD方法能够成功获得脑GM的纤维方向,并在三维空间中进行了重建.与传统的NODDI-CSD方法相比,基于SANDI的GM-MSCSD方法能够更准确地估计GM区域的纤维结构,实现了精确的GM微结构成像.综上所述,本文提出的基于SANDI的GM-MSCSD方法是对传统CSD方法的重要补充和改进.通过充分考虑GM内部的各向异性扩散特性,该方法能够更准确地揭示GM的微观结构,为神经科学研究提供了有力的技术支持.
利益冲突
无
参考文献
A fiber tracking algorithm based on non-local constrained spherical deconvolution
[J].
基于非局部约束球面反卷积模型的纤维追踪算法
[J].
DOI:10.11938/cjmr20192798
[本文引用: 1]

基于扩散磁共振成像的纤维追踪技术为非侵入性观测脑白质结构提供了有力的手段,约束球面反卷积作为一种多纤维追踪模型,能够对体素内纤维的方向信息进行建模,进而实现脑纤维的重构.针对约束球面反卷积模型的不适定性以及细节信息丢失问题,本文在约束球面反卷积的基础上,结合邻域信息和分数阶正则化,提出了一种基于非局部约束球面反卷积模型的确定型纤维追踪算法,分数阶的非局部特性使得纤维方向分布模型估计的误差更小,而邻域信息的引入保证了空间一致性,可以减少噪声的影响.分别利用模拟数据、人脑实际数据对本文算法及基于约束球面反卷积的确定型纤维追踪算法作对比实验,结果表明,利用本文算法追踪的纤维不仅整体视觉效果上较整洁,而且对交叉纤维的重建结果更完整准确.
A model-based deconvolution approach to solve fiber crossing in diffusion-weighted MR imaging
[J].
Construction of human brain templates with diffusion tensor imaging data: a review
[J].
扩散张量成像的人脑模板构建
[J].
DOI:10.11938/cjmr20182662
[本文引用: 1]

扩散张量脑模板包含丰富的大脑白质组织信息,在空间标准化或者脑图谱创建中具有重要价值,然而基于扩散张量模型构建的脑模板精度不高,特别是在脑部复杂的神经元微观结构区域中应用受到限制.针对这一问题,研究者们提出了基于高分辨率扩散成像构建大脑模板的方法.本文对使用扩散张量成像方法进行脑模板构建的研究进展进行了综述,首先介绍了扩散张量脑模板构建的发展进程,阐述了脑模板构建中解决的技术问题及同时存在的局限性;接着详细论述了基于扩散频谱成像及高角度分辨率扩散成像构建脑模板的不同方法间的差异,并总结了这些研究方法取得的重要进展;最后通过分析目前研究进展提出该研究问题中存在的不足以及未来的发展趋势.
Constrained spherical deconvolution tractography reveals cerebello-mammillary connections in humans
[J].
Generalized Richardson-Lucy (GRL) for analyzing multi-shell diffusion MRI data
[J].
A framework for multi-component analysis of diffusion MRI data over the neonatal period
[J].
DOI:S1053-8119(18)32032-9
PMID:30391562
[本文引用: 1]

We describe a framework for creating a time-resolved group average template of the developing brain using advanced multi-shell high angular resolution diffusion imaging data, for use in group voxel or fixel-wise analysis, atlas-building, and related applications. This relies on the recently proposed multi-shell multi-tissue constrained spherical deconvolution (MSMT-CSD) technique. We decompose the signal into one isotropic component and two anisotropic components, with response functions estimated from cerebrospinal fluid and white matter in the youngest and oldest participant groups, respectively. We build an orientationally-resolved template of those tissue components from data acquired from 113 babies between 33 and 44 weeks postmenstrual age, imaged as part of the Developing Human Connectome Project. These data were split into weekly groups, and registered to the corresponding group average templates using a previously-proposed non-linear diffeomorphic registration framework, designed to align orientation density functions (ODF). This framework was extended to allow the use of the multiple contrasts provided by the multi-tissue decomposition, and shown to provide superior alignment. Finally, the weekly templates were registered to the same common template to facilitate investigations into the evolution of the different components as a function of age. The resulting multi-tissue atlas provides insights into brain development and accompanying changes in microstructure, and forms the basis for future longitudinal investigations into healthy and pathological white matter maturation.Copyright © 2018 The Authors. Published by Elsevier Inc. All rights reserved.
Single-shell to multi-shell dMRI transformation using spatial and volumetric multilevel hierarchical reconstruction framework
[J].
Multi-tissue constrained spherical deconvolution for improved analysis of multi-shell diffusion MRI data
[J].
DOI:S1053-8119(14)00644-2
PMID:25109526
[本文引用: 2]

Constrained spherical deconvolution (CSD) has become one of the most widely used methods to extract white matter (WM) fibre orientation information from diffusion-weighted MRI (DW-MRI) data, overcoming the crossing fibre limitations inherent in the diffusion tensor model. It is routinely used to obtain high quality fibre orientation distribution function (fODF) estimates and fibre tractograms and is increasingly used to obtain apparent fibre density (AFD) measures. Unfortunately, CSD typically only supports data acquired on a single shell in q-space. With multi-shell data becoming more and more prevalent, there is a growing need for CSD to fully support such data. Furthermore, CSD can only provide high quality fODF estimates in voxels containing WM only. In voxels containing other tissue types such as grey matter (GM) and cerebrospinal fluid (CSF), the WM response function may no longer be appropriate and spherical deconvolution produces unreliable, noisy fODF estimates. The aim of this study is to incorporate support for multi-shell data into the CSD approach as well as to exploit the unique b-value dependencies of the different tissue types to estimate a multi-tissue ODF. The resulting approach is dubbed multi-shell, multi-tissue CSD (MSMT-CSD) and is compared to the state-of-the-art single-shell, single-tissue CSD (SSST-CSD) approach. Using both simulations and real data, we show that MSMT-CSD can produce reliable WM/GM/CSF volume fraction maps, directly from the DW data, whereas SSST-CSD has a tendency to overestimate the WM volume in voxels containing GM and/or CSF. In addition, compared to SSST-CSD, MSMT-CSD can substantially increase the precision of the fODF fibre orientations and reduce the presence of spurious fODF peaks in voxels containing GM and/or CSF. Both effects translate into more reliable AFD measures and tractography results with MSMT-CSD compared to SSST-CSD.Copyright © 2014 Elsevier Inc. All rights reserved.
Multi-tissue spherical deconvolution of tensor-valued diffusion MRI
[J].
Using diffusion anisotropy to study cerebral cortical gray matter development
[J].
DOI:S1090-7807(18)30115-0
PMID:29705039
[本文引用: 1]

Diffusion-weighted magnetic resonance imaging (diffusion MRI) is being used to characterize morphological development of cells within developing cerebral cortical gray matter. Abnormal morphology is a shared characteristic of cerebral cortical neurons for many neurodevelopmental disorders, and therefore diffusion MRI is potentially of high value for monitoring growth-related anatomical changes of relevance to brain function. Here, the theoretical framework for analyzing diffusion MRI data is summarized. An overview of quantitative methods for validating the interpretations of diffusion MRI data using light microscopy is then presented. These theoretical modeling and validation methods have been used to precisely characterize changes in water diffusion anisotropy with development in the context of several animal model systems. Further, in diffusion MRI studies of several preclinical models of neurodevelopmental disorders, the ability is demonstrated of diffusion MRI to detect abnormal morphological neural development. These animal model studies are reviewed along with recent initial efforts to translate the findings into an approach for studies of human subjects. This body of data indicates that diffusion MRI has the requisite sensitivity to detect abnormal cellular development in the context of several models of neurodevelopmental disorders, and therefore may provide a new strategy for detecting abnormalities in early stages of brain development in humans.Copyright © 2018. Published by Elsevier Inc.
Imaging laminar structures in the gray matter with diffusion MRI
[J].
DOI:S1053-8119(17)31120-5
PMID:29309898
[本文引用: 1]

The cortical layers define the architecture of the gray matter and its neuroanatomical regions and are essential for brain function. Abnormalities in cortical layer development, growth patterns, organization, or size can affect brain physiology and cognition. Unfortunately, while large population studies are underway that will greatly increase our knowledge about these processes, current non-invasive techniques for characterizing the cortical layers remain inadequate. For decades, high-resolution T1 and T2 Weighted Magnetic Resonance Imaging (MRI) have been the method-of-choice for gray matter and layer characterization. In the past few years, however, diffusion MRI has shown increasing promise for its unique insights into the fine structure of the cortex. Several different methods, including surface analysis, connectivity exploration, and sub-voxel component modeling, are now capable of exploring the diffusion characteristics of the cortex. In this review, we will discuss current advances in the application of diffusion imaging for cortical characterization and its unique features, with a particular emphasis on its spatial resolution, arguably its greatest limitation. In addition, we will explore the relationship between the diffusion MRI signal and the cellular components of the cortex, as visualized by histology. While the obstacles facing the widespread application of cortical diffusion imaging remain daunting, the information it can reveal may prove invaluable. Within the next few years, we predict a surge in the application of this technique and a concomitant expansion of our knowledge of cortical layers.Copyright © 2018 Elsevier Inc. All rights reserved.
Composite hindered and restricted model of diffusion (CHARMED) MR imaging of the human brain
[J].
DOI:10.1016/j.neuroimage.2005.03.042
PMID:15979342
[本文引用: 1]

High b value diffusion-weighted images sampled at high angular resolution were analyzed using a composite hindered and restricted model of diffusion (CHARMED). Measurements and simulations of diffusion in white matter using CHARMED provide an unbiased estimate of fiber orientation with consistently smaller angular uncertainty than when calculated using a DTI model or with a dual tensor model for any given signal-to-noise level. Images based on the population fraction of the restricted compartment provide a new contrast mechanism that enhances white matter like DTI. Nevertheless, it is assumed that these images might be more sensitive than DTI to white matter disorders. We also provide here an experimental design and analysis framework to implement CHARMED MRI that is feasible on human clinical scanners.
NODDI: Practical in vivo neurite orientation dispersion and density imaging of the human brain
[J].
DOI:10.1016/j.neuroimage.2012.03.072
PMID:22484410
[本文引用: 1]

This paper introduces neurite orientation dispersion and density imaging (NODDI), a practical diffusion MRI technique for estimating the microstructural complexity of dendrites and axons in vivo on clinical MRI scanners. Such indices of neurites relate more directly to and provide more specific markers of brain tissue microstructure than standard indices from diffusion tensor imaging, such as fractional anisotropy (FA). Mapping these indices over the whole brain on clinical scanners presents new opportunities for understanding brain development and disorders. The proposed technique enables such mapping by combining a three-compartment tissue model with a two-shell high-angular-resolution diffusion imaging (HARDI) protocol optimized for clinical feasibility. An index of orientation dispersion is defined to characterize angular variation of neurites. We evaluate the method both in simulation and on a live human brain using a clinical 3T scanner. Results demonstrate that NODDI provides sensible neurite density and orientation dispersion estimates, thereby disentangling two key contributing factors to FA and enabling the analysis of each factor individually. We additionally show that while orientation dispersion can be estimated with just a single HARDI shell, neurite density requires at least two shells and can be estimated more accurately with the optimized two-shell protocol than with alternative two-shell protocols. The optimized protocol takes about 30 min to acquire, making it feasible for inclusion in a typical clinical setting. We further show that sampling fewer orientations in each shell can reduce the acquisition time to just 10 min with minimal impact on the accuracy of the estimates. This demonstrates the feasibility of NODDI even for the most time-sensitive clinical applications, such as neonatal and dementia imaging.Copyright © 2012 Elsevier Inc. All rights reserved.
SANDI: a compartment-based model for non-invasive apparent soma and neurite imaging by diffusion MRI
[J].
Review of brain microstructural imaging with diffusion magnetic resonance imaging
[J].Microstructure imaging is a technique based on diffusion magnetic resonance imaging to characterize the microstructure of human brain tissue in vivo.It has been widely used in neuroscience research and clinical application.The microstructure imaging model correlates different tissue properties and magnetic resonance signals to estimate the microscopic properties of the tissue.This paper first introduces the research status and shortcomings of microstructure imaging,then summarizes the classical brain microstructure imaging methods from the perspective of signal model and multi compartment model,summarizes the advantages and disadvantages of these two types of models,and introduces the quantitative analysis methods of microstructure.Finally,the microstructure imaging technology is summarized and prospected.
扩散磁共振图像的大脑微结构成像研究综述
[J].微结构成像是基于扩散磁共振成像在活体内表征人脑组织微结构特性的技术,现已被广泛应用于神经科学研究和临床应用中.微结构成像模型将不同组织特性和磁共振信号相关联以估算组织的微观特性.本文首先介绍微结构成像的研究现状及不足,之后从信号模型与多隔室模型两个角度综述了经典的大脑微结构成像方法,总结这两类模型存在的优点及不足,并介绍微结构量化分析方法,最后对微结构成像技术进行总结和展望.
Modeling dendrite density from magnetic resonance diffusion measurements
[J].
DOI:10.1016/j.neuroimage.2006.10.037
PMID:17188901
[本文引用: 1]

Diffusion-weighted imaging (DWI) provides a noninvasive tool to probe tissue microstructure. We propose a simplified model of neural cytoarchitecture intended to capture the essential features important for water diffusion as measured by NMR. Two components contribute to the NMR signal in this model: (i) the dendrites and axons, which are modeled as long cylinders with two diffusion coefficients, parallel (D(L)) and perpendicular (D(T)) to the cylindrical axis, and (ii) an isotropic monoexponential diffusion component describing water diffusion within and across all other structures, i.e., in extracellular space and glia cells. The model parameters are estimated from 153 diffusion-weighted images acquired from a formalin-fixed baboon brain. A close correspondence between the data and the signal model is found, with the model parameters consistent with literature values. The model provides an estimate of dendrite density from noninvasive MR diffusion measurements, a parameter likely to be of value for understanding normal as well as abnormal brain development and function.
White matter characterization with diffusional kurtosis imaging
[J].
DOI:10.1016/j.neuroimage.2011.06.006
PMID:21699989
[本文引用: 1]

Diffusional kurtosis imaging (DKI) is a clinically feasible extension of diffusion tensor imaging that probes restricted water diffusion in biological tissues using magnetic resonance imaging. Here we provide a physically meaningful interpretation of DKI metrics in white matter regions consisting of more or less parallel aligned fiber bundles by modeling the tissue as two non-exchanging compartments, the intra-axonal space and extra-axonal space. For the b-values typically used in DKI, the diffusion in each compartment is assumed to be anisotropic Gaussian and characterized by a diffusion tensor. The principal parameters of interest for the model include the intra- and extra-axonal diffusion tensors, the axonal water fraction and the tortuosity of the extra-axonal space. A key feature is that these can be determined directly from the diffusion metrics conventionally obtained with DKI. For three healthy young adults, the model parameters are estimated from the DKI metrics and shown to be consistent with literature values. In addition, as a partial validation of this DKI-based approach, we demonstrate good agreement between the DKI-derived axonal water fraction and the slow diffusion water fraction obtained from standard biexponential fitting to high b-value diffusion data. Combining the proposed WM model with DKI provides a convenient method for the clinical assessment of white matter in health and disease and could potentially provide important information on neurodegenerative disorders.Copyright © 2011 Elsevier Inc. All rights reserved.
Quantitative mapping of the per-axon diffusion coefficients in brain white matter
[J].
DOI:10.1002/mrm.25734
PMID:25974332
[本文引用: 1]

This article presents a simple method for estimating the effective diffusion coefficients parallel and perpendicular to the axons unconfounded by the intravoxel fiber orientation distribution. We also call these parameters the per-axon or microscopic diffusion coefficients.Diffusion MR imaging is used to probe the underlying tissue material. The key observation is that for a fixed b-value the spherical mean of the diffusion signal over the gradient directions does not depend on the axon orientation distribution. By exploiting this invariance property, we propose a simple, fast, and robust estimator of the per-axon diffusion coefficients, which we refer to as the spherical mean technique.We demonstrate quantitative maps of the axon-scale diffusion process, which has factored out the effects due to fiber dispersion and crossing, in human brain white matter. These microscopic diffusion coefficients are estimated in vivo using a widely available off-the-shelf pulse sequence featuring multiple b-shells and high-angular gradient resolution.The estimation of the per-axon diffusion coefficients is essential for the accurate recovery of the fiber orientation distribution. In addition, the spherical mean technique enables us to discriminate microscopic tissue features from fiber dispersion, which potentially improves the sensitivity and/or specificity to various neurological conditions. Magnetic Resonance in Medicine published by Wiley Periodicals, Inc.© 2015 The Authors. Magnetic Resonance in Medicine published by Wiley Periodicals, Inc.
Intracellular water preexchange lifetime in neurons and astrocytes
[J].
DOI:10.1002/mrm.26781
PMID:28675497
[本文引用: 1]

To determine the intracellular water preexchange lifetime, τ, the "average residence time" of water, in the intracellular milieu of neurons and astrocytes. The preexchange lifetime is important for modeling a variety of MR data sets, including relaxation, diffusion-sensitive, and dynamic contrast-enhanced data sets.Herein, τ in neurons and astrocytes is determined in a microbead-adherent, cultured cell system. In concert with thin-slice selection, rapid flow of extracellular media suppresses extracellular signal, allowing determination of the transcytolemmal-exchange-dominated, intracellular T. With this knowledge, and that of the intracellular T in the absence of exchange, τ can be derived.Under normal culture conditions, τ for neurons is 0.75 ± 0.05 s versus 0.57 ± 0.03 s for astrocytes. Both neuronal and astrocytic τ s decrease within 30 min after the onset of oxygen-glucose deprivation, with the astrocytic τ showing a substantially greater decrease than the neuronal τ.Given an approximate intra- to extracellular volume ratio of 4:1 in the brain, these data imply that, under normal physiological conditions, an MR experimental characteristic time of less than 0.012 s is required for a nonexchanging, two-compartment (intra- and extracellular) model to be valid for MR studies. This characteristic time shortens significantly (i.e., 0.004 s) under injury conditions. Magn Reson Med 79:1616-1627, 2018. © 2017 International Society for Magnetic Resonance in Medicine.© 2017 International Society for Magnetic Resonance in Medicine.
A modified damped Richardson-Lucy algorithm to reduce isotropic background effects in spherical deconvolution
[J].
DOI:10.1016/j.neuroimage.2009.09.033
PMID:19781650
[本文引用: 2]

Spherical deconvolution methods have been applied to diffusion MRI to improve diffusion tensor tractography results in brain regions with multiple fibre crossing. Recent developments, such as the introduction of non-negative constraints on the solution, allow a more accurate estimation of fibre orientations by reducing instability effects due to noise robustness. Standard convolution methods do not, however, adequately model the effects of partial volume from isotropic tissue, such as gray matter, or cerebrospinal fluid, which may degrade spherical deconvolution results. Here we use a newly developed spherical deconvolution algorithm based on an adaptive regularization (damped version of the Richardson-Lucy algorithm) to reduce isotropic partial volume effects. Results from both simulated and in vivo datasets show that, compared to a standard non-negative constrained algorithm, the damped Richardson-Lucy algorithm reduces spurious fibre orientations and preserves angular resolution of the main fibre orientations. These findings suggest that, in some brain regions, non-negative constraints alone may not be sufficient to reduce spurious fibre orientations. Considering both the speed of processing and the scan time required, this new method has the potential for better characterizing white matter anatomy and the integrity of pathological tissue.
Spherical deconvolution with tissue-specific response functions and multi-shell diffusion MRI to estimate multiple fiber orientation distributions (mFODs)
[J].
Robust determination of the fibre orientation distribution in diffusion MRI: non-negativity constrained super-resolved spherical deconvolution.
[J].
DOI:10.1016/j.neuroimage.2007.02.016
PMID:17379540
[本文引用: 1]

Diffusion-weighted (DW) MR images contain information about the orientation of brain white matter fibres that potentially can be used to study human brain connectivity in vivo using tractography techniques. Currently, the diffusion tensor model is widely used to extract fibre directions from DW-MRI data, but fails in regions containing multiple fibre orientations. The spherical deconvolution technique has recently been proposed to address this limitation. It provides an estimate of the fibre orientation distribution (FOD) by assuming the DW signal measured from any fibre bundle is adequately described by a single response function. However, the deconvolution is ill-conditioned and susceptible to noise contamination. This tends to introduce artefactual negative regions in the FOD, which are clearly physically impossible. In this study, the introduction of a constraint on such negative regions is proposed to improve the conditioning of the spherical deconvolution. This approach is shown to provide FOD estimates that are robust to noise whilst preserving angular resolution. The approach also permits the use of super-resolution, whereby more FOD parameters are estimated than were actually measured, improving the angular resolution of the results. The method provides much better defined fibre orientation estimates, and allows orientations to be resolved that are separated by smaller angles than previously possible. This should allow tractography algorithms to be designed that are able to track reliably through crossing fibre regions.
Measurement of fiber orientation distributions using high angular resolution diffusion imaging
[J].High angular resolution measurements of diffusion are used to estimate the angular distribution and diffusion anisotropy of fibers in a voxel. A simple, axially symmetric model of diffusion in white matter fibers is used to relate diffusion measurements to fiber properties. The new technique is called fiber orientation estimated using continuous axially symmetric tensors (FORECAST). It is tested using both numerical simulation and in vivo measurements. The new method agrees with other methods in voxels containing single fibers, but resolves crossing fibers better, at least at the level of diffusion weighting used in this study (tr(b) = 1480 s/mm2). The simplifying assumptions of the model are tested by comparison with the "model-free" q-ball analysis of in vivo data and the results are shown to be in good agreement. The new method addresses the problem of partial volume averaging in diffusion tensor imaging and provides a basis for more reliable estimates of fiber orientation and fractional anisotropy.(c) 2005 Wiley-Liss, Inc.
SpinDoctor: a Matlab toolbox for diffusion MRI simulation
[J].
Diffusion MRI simulation of realistic neurons with SpinDoctor and the Neuron Module
[J].
Spin diffusion measurements: spin echoes in the presence of a time-dependent field gradient
[J].
Accelerated microstructure imaging via convex optimization (AMICO) from diffusion MRI data
[J].
DOI:10.1016/j.neuroimage.2014.10.026
PMID:25462697
[本文引用: 1]

Microstructure imaging from diffusion magnetic resonance (MR) data represents an invaluable tool to study non-invasively the morphology of tissues and to provide a biological insight into their microstructural organization. In recent years, a variety of biophysical models have been proposed to associate particular patterns observed in the measured signal with specific microstructural properties of the neuronal tissue, such as axon diameter and fiber density. Despite very appealing results showing that the estimated microstructure indices agree very well with histological examinations, existing techniques require computationally very expensive non-linear procedures to fit the models to the data which, in practice, demand the use of powerful computer clusters for large-scale applications. In this work, we present a general framework for Accelerated Microstructure Imaging via Convex Optimization (AMICO) and show how to re-formulate this class of techniques as convenient linear systems which, then, can be efficiently solved using very fast algorithms. We demonstrate this linearization of the fitting problem for two specific models, i.e. ActiveAx and NODDI, providing a very attractive alternative for parameter estimation in those techniques; however, the AMICO framework is general and flexible enough to work also for the wider space of microstructure imaging methods. Results demonstrate that AMICO represents an effective means to accelerate the fit of existing techniques drastically (up to four orders of magnitude faster) while preserving accuracy and precision in the estimated model parameters (correlation above 0.9). We believe that the availability of such ultrafast algorithms will help to accelerate the spread of microstructure imaging to larger cohorts of patients and to study a wider spectrum of neurological disorders. Copyright © 2014 The Authors. Published by Elsevier Inc. All rights reserved.