引言
磁共振指纹(Magnetic Resonance Fingerprinting,MRF)成像由凯斯西储大学的Mark Griswold教授团队于2013年首次提出[1 ,2 ] .该技术通过伪随机脉冲激发受检组织,使不同组织生成独特的时变暂态弛豫响应信号,即MRF信号.在频域完成数据采集后,通过逆傅里叶变换重建获得时域信号.同时,基于磁共振信号激发的布洛赫方程,构建一个包含各种人体组织理论MRF信号的字典.通过模式匹配算法,将重建信号与字典中的理论信号进行比对,从而获得多个定量参数,例如自旋-晶格弛豫时间(Spin-lattice Relaxation Time,T 1 )和自旋-自旋弛豫时间(Spin-spin Relaxation Time,T 2 ).这些定量参数能够客观反映组织的生理状态及病理变化,为疾病的早期诊断和疗效评估提供了重要依据.前瞻性临床应用研究表明,MRF成像技术在心脑血管、肿瘤及神经系统等疾病[3 -4 ] 的早期诊断和病理分级方面中展现出显著优势. 然而,为提升信号特异性并加速数据采集,MRF成像通常采用高倍欠采样策略,仅采集少量数据(约2%~8%)[5 ] 用于定量成像. 这导致逆傅里叶变换重建的时域MRF图像中出现严重的混叠伪影,进而降低定量成像的精度.
近年来,研究者们已相继提出多种重建方法,旨在克服欠采样伪影的影响,进而提升定量成像精度.Davis等[6 ] 提出了一种在压缩感知理论框架下应用的布洛赫响应流形投影方法(Bloch Response Recovery via Iterative Projection,BLIP),有效利用指纹字典内的先验信息,优化数据重建质量.Zhao等[7 ] 则提出了基于最大似然估计的重建方法(MBIR),旨在直接从高度欠采样的测量数据中精确估计定量参数图.然而,上述方法在很大程度上忽略了MRF数据在时间和空间维度上的相关性,限制了定量成像精度的进一步提升.为此,最新的研究工作聚焦于充分挖掘MRF数据的时-空相关冗余,以期进一步提升重建质量.Mazor等[8 ] 提出了一种基于低秩与子空间投影的重建方法(FLOR),将MRF数据按时间帧列化为二维低秩矩阵,有效提升了重建的质量与速度.此后,Zhao等[9 ] 进一步引入低秩张量模型,显著缓解了低秩重建方法中矩阵预处理步骤可能导致的信息损失问题.Cruz等[10 ] 则开发了一种融合稀疏性和局部低秩正则化的重建方法,实现了更短的扫描时间和更高的空间分辨率.Hu等[11 ] 提出了结构化低秩矩阵补全与子空间投影框架(Structured Low-rank Matrix Completion and Subspace Projection,SL-SP),旨在从高度欠采样的测量数据中恢复高质量的MRF数据,从而提升定量成像精度.总体而言,现有方法主要依赖于数据先验模型,并充分利用MRF数据的低秩性、稀疏性及平滑性[12 ] 等固有特性,进而在压缩感知理论框架下进行模型优化,以有效抑制欠采样伪影并重建高质量时域图像.然而,值得关注的是,基于数据先验的约束模型难以充分表征布洛赫成像模型中复杂的时间维度特征,且在定量精度与计算效率之间依然存在难以调和的矛盾,难以兼顾临床应用对实时性和高精度的双重需求.
除上述致力于提升MRF数据重建质量的研究方向外,另一些研究工作则着眼于改进模式匹配方法,以期实现高精度的参数量化.McGivney等[13 ] 提出利用奇异值分解将字典和体素指纹投影到时间域上的低维子空间,并在低维子空间中进行模式匹配,从而有效减少了匹配时间和计算开销.Yang等[14 ] 进一步提出使用随机奇异值分解直接估计低维字典子空间,进一步降低了模式匹配的计算时间,并有效减少了指纹字典的内存需求.然而,必须指出的是,基于字典压缩的方法不可避免地会造成部分信息的丢失,进而在一定程度上牺牲了参数估计的精度.为了有效解决这一问题,基于深度学习的方法逐渐成为MRF成像中模式匹配方法的主流方案.Cohen等[15 ] 提出了一种四层全连接神经网络,用于构建信号到参数的映射,有效取代了占用大量内存的字典和计算耗时的字典匹配过程.Oksuz等[16 ] 提出了一种循环神经网络,充分利用组织指纹的时间维度相关信息,有效提高定量成像的精度.Fang等[17 ] 设计了一种两段式深度学习模型(SCQ),整合了全连接网络与U-Net,在四倍加速采集条件下实现了精准的参数重建.Soyak等[18 ] 则提出了一种包含通道注意力模块和全卷积网络的神经网络,并进一步采用重叠块策略进行块级多参数估计,从而有效地减少了参数重建误差.然而,深度学习技术在MRF领域的应用依然受到大规模训练数据集需求的限制,且模型训练与优化依然面临挑战.此外,现有研究大多采用传统图像处理领域业已成熟的网络结构,其在MRF成像领域的泛化能力仍有待进一步验证.
近年来,流形理论凭借其卓越的高维数据低维表征能力,在动态磁共振成像领域得到了日益广泛的应用[19 30] .基于流形的方法将连续图像帧或离散测量值抽象为嵌入高维空间中的低维流形上的数据点,并有效利用非线性和非局部流形结构正则化来显著提升重建性能.Poddar等[24 ] 提出了一种开创性的动态磁共振成像方法(SToRM),创新性地通过将图像帧建模为高维空间中光滑低维流形上的离散点集,充分利用数据中的非线性和非局部冗余信息来提升重建性能.在后续研究中,SToRM方法被进一步扩展到带限图像流形[23 ] 和无导航先验流形[24 ] 等多种应用场景.Nakarmi等[27 ] 巧妙地利用核主成分分析方法学习特征空间主成分所描述的潜在流形,并进一步通过特征空间中的低秩约束强化这种结构,从而有效加速了动态磁共振成像.基于流形结构的重建方法在有效挖掘高维数据中的非局部和非线性结构信息方面已然展现了巨大的潜力[28 ] .然而,在实际应用中,在噪声和欠采样伪影的双重干扰下,如何从采集到的高维数据观测样本中准确且稳健地估计潜在流形结构仍然极具挑战.
为此,本文提出了一种基于流形结构正则化的MRF重建方法.该方法将指纹信号与组织定量参数建模为流形上的点,并揭示了指纹流形与参数流形之间内在拓扑结构的一致性.基于这一发现,本文提出MRF成像的流形结构正则化约束,旨在通过在重建过程中显式地约束指纹流形与参数流形的结构一致性以提高重建质量.此外,该方法还整合了局部低秩先验,以充分利用每个数据块内的局部相关性并进一步提升重建性能.实验结果证实,相较于现有最先进的重建方法,本文方法能够在大幅减少计算时间的同时实现更优的重建性能.本文的主要贡献总结如下:
(1)MRF的流形结构正则化:将指纹信号与组织定量参数建模为流形上的点,并首次揭示了指纹流形与参数流形之间内在拓扑结构的一致性.
(2)显式流形结构估计:提出通过低维参数流形上对应点之间的欧式距离来估MRF数据的潜在流形结构,无需额外信息即可显式且可靠地表征指纹流形的内在结构.
(3)统一优化框架:与传统的两步处理流程(即通过特定数据重建方法先恢复时域MRF数据,再基于模式匹配估计参数图)不同,本文提出的方法通过流形结构正则化将这两个步骤整合到一个统一的优化框架中,有效提高了定量成像的准确性.
1 研究背景
1.1 流形基本理论
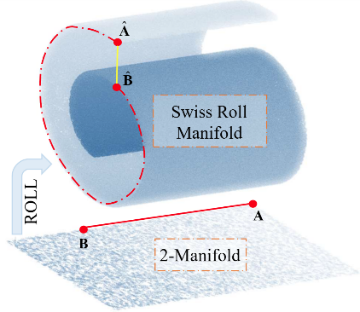
流形假设指出,现实世界中的高维观测数据本质上是低维流形在高维欧式空间中的非线性嵌入[19 ,21 -22 ] ,流形的维度通常远低于其所在欧式空间的维度,为便于区分,本文中以n -流形特指维度为n 的低维流形. 图1 展示了经典的瑞士卷流形,其表示一个嵌入在三维欧式空间中的2-流形.从几何上看,该流形本质上是将二维平面在三维欧氏空间中卷曲形成的.瑞士卷流形直观地展示了数据内在结构与外在表现之间的复杂关系.在高维空间中,两点之间的欧式距离往往无法准确反映它们的内在相似性[19 ] .以瑞士卷流形上的两个点$\hat{A}$ $\hat{B}$ 图1 中的黄色实线)显著小于其在流形上的实际距离(红色虚线),其实际距离需要通过流形上的测地距离(红色虚线),或将流形映射回低维平面后再以欧氏距离来精确衡量(A 和B 间红色实线).前者要求对流形的潜在拓扑结构进行精确估计,而后者则依赖于适当的数据降维方法,从其高维嵌入中恢复流形的原始结构.然而,在实际应用中,确定潜在流行的维度并准确估计流形结构仍然是十分困难的问题,这一方面,这需要海量的观测数据以及对数据的充分先验信息;另一方面,退化的观测数据所导致的估计偏差亦会产生显著影响.具体而言,噪声会干扰流形结构的识别,而欠采样则可能导致数据分布的稀疏性和不完整性,从而进一步增加流形建模的难度.
图1
图1
瑞士卷流形的示意图:嵌入在三维空间中的2-流形
Fig. 1
Illustration of the well-known Swiss roll manifold: 2-manifold embedded in 3D space
1.2 MRF重建模型
MRF成像中的数据采集[5 ] 可以表示为如下线性模型:
(1) $\mathbf{b}=\mathsf{\mathcal{A}\mathcal{X}}+\mathbf{n}$
其中,$\mathbf{b}\in {{\mathbb{C}}^{{{N}_{c}}\times {{N}_{s}}\times L}}$ k 空间测量数据,包含来自${{N}_{c}}$ ${{N}_{s}}$ k 空间样本数量,L 是时间帧的数量.$\mathsf{\mathcal{X}}\in {{\mathbb{C}}^{{{N}_{x}}\times {{N}_{y}}\times L}}$ ${{N}_{x}}$ ${{N}_{y}}$ $\mathbf{n}\in {{\mathbb{C}}^{{{N}_{c}}\times {{N}_{s}}\times L}}$ $\mathsf{\mathcal{A}}={{\mathbf{F}}_{u}}\mathbf{C}$ $\mathbf{C}$ ${{\mathbf{F}}_{u}}$ .
根据MRF成像机理[6 ] ,MRF数据$\mathsf{\mathcal{X}}$
(2) ${{\mathsf{\mathcal{X}}}_{i,j,:}}={{\rho }_{i,j}}\mathbf{B}({{\text{ }\!\!\eta\!\!\text{ }}_{i,j}},\theta )$
其中,${{\rho }_{i,j}}\in {{\mathbb{R}}_{+}}$ ${{\eta }_{i,j}}=[{{T}_{1}},{{T}_{2}},\cdots ]$ $\theta $ $\mathbf{B}(\cdot ):{{\mathbb{R}}^{2}}\to {{\mathbb{C}}^{L}}$ $\mathsf{\mathcal{B}}$ [6 ] .本文中主要考虑三个关键组织参数:纵向弛豫时间 (T 1 )、横向弛豫时间(T 2 )和质子密度(PD),并将有所有可能的组织参数组合构成的数据空间建模为三维参数流形$\mathsf{\mathcal{M}}\in {{\mathbb{R}}^{3}}$ .
MRF成像的另一个关键部分在于基于模式匹配的参数量化,这需要预先构建组织指纹字典,包含尽可能多的组织的理论指纹信号,指纹字典可以建模为:
(3) $\mathbf{D}=\{{{\mathbf{d}}_{m,:}}\},\quad \ \ \ {{\mathbf{d}}_{m,:}}=\mathbf{B}({{\eta }_{m}},\theta )\in {{\mathbb{C}}^{1\times L}}$
其中,$\{{{\eta }_{m}},\ m=1,\cdots,M\}$ $\mathsf{\mathcal{M}}$ $\mathbf{D}$ $\mathbf{D}$ $\mathsf{\mathcal{B}}$ [6 ] 的离散化近似.多参数定量图像可以通过将重建的MRF数据$\mathsf{\hat{\mathcal{X}}}$ [1 ] ,这一过程可以表示为:$\hat{M}={{\Phi }_{\mathbf{D}}}(\mathsf{\hat{\mathcal{X}}})$ $\hat{M}$ ${{\Phi }_{\mathbf{D}}}(\cdot )$ [1 ,11 ] 可以通过预计算的字典$\mathbf{D}$
2 方法
2.1 流形结构正则化
布洛赫流形$\mathsf{\mathcal{B}}$ L 维欧式空间中的一个2-流形,其中L 表示指纹信号的帧长度.此外,本文用$\mathsf{\mathcal{S}}$ $\mathsf{\mathcal{S}}$ $\mathsf{\mathcal{B}}$ [6 ,31 ] ,是嵌入在L 维空间中的一个3-流形.表1 中列出了本文使用的流形相关的重要符号及其定义.
根据皮卡-林德洛夫(Picard-Lindelöf)定理[32 ] ,对于任意组织参数组合,其对应的理论指纹响应信号是唯一的.也即,若存在两个不同的组织参数组合${{\eta }_{i}}$ ${{\eta }_{j}}$ ${{\eta }_{i}}={{\eta }_{j}}$
(4) $\mathbf{B}({{\eta }_{i}},\theta )=\mathbf{B}({{\eta }_{j}},\theta )\Leftrightarrow {{\eta }_{i}}={{\eta }_{j}}$
此外,布洛赫方程在组织参数和指纹响应信号之间建立了稳定的非线性映射[32 ] ,即:
(5) $\left\| \mathbf{B}({{\eta }_{i}},\theta )\ -\ \mathbf{B}({{\eta }_{j}},\theta ) \right\|_{F}^{2}\le \delta \Rightarrow \left\| {{\eta }_{i}}-{{\eta }_{j}} \right\|_{2}^{2}\le C\delta $
其中,$\|\cdot {{\|}_{F}}$ $\delta $ C > 0为与$\delta $ $\mathsf{\mathcal{S}}$ $\mathsf{\mathcal{M}}$ $\mathsf{\mathcal{S}}$ $\mathsf{\mathcal{M}}$
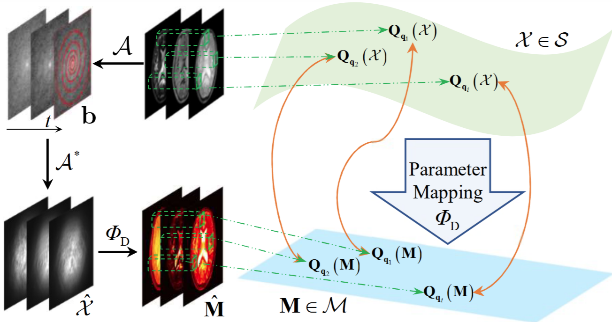
图2 展示了本文所提出的流形结构化正则化先验的构建示意图,其核心思想在于以局部空间块为基本单元估计MRF数据的潜在流形结构.这一策略基于以下两点考虑:(1)混叠伪影和噪声干扰下,体素级的指纹信号受到不同程度的影响,直接进行流形结构估计易出现不同程度的偏差,降低算法性能;(2)MRF成像通常具有高分辨率特性,体素级建模会显著增加流形结构估计的计算复杂度与计算开销.具体而言,高维MRF数据被划分为重叠的局部空间块,而数据块之间的相似性度量通过低维参数流形中对应块之间的欧式距离来估计.所提出的流形结构化正则化先验能够挖掘MRF数据中的非线性和非局部冗余信息,并提高欠采样和噪声场景下流形结构估计的准确性.所提出的流形结构化数据正则化项${{\mathsf{\mathcal{J}}}_{\text{MS}}}(\mathsf{\mathcal{X}})$
(6) ${{\mathsf{\mathcal{J}}}_{\text{MS}}}(\mathsf{\mathcal{X}})=\sum\limits_{i}{\sum\limits_{j}{{{w}_{i,j}}}}\left\| {{\mathbf{Q}}_{{{\mathbf{q}}_{i}}}}(\mathsf{\mathcal{X}})-{{\mathbf{Q}}_{{{\mathbf{q}}_{j}}}}(\mathsf{\mathcal{X}}) \right\|_{F}^{2},\ \ \ i\ne j$
图2
图2
流形结构化正则化先验构建示意图
Fig. 2
Illustration of the proposed manifold structured data regularization scheme
其中,i 和j 表示数据块的索引;${{w}_{i,j}}$ ${{\mathbf{Q}}_{{{\mathbf{q}}_{k}}}}(\cdot )$ ${{\mathbf{q}}_{k}}$ ${{\mathbf{Q}}_{{{\mathbf{q}}_{k}}}}(\mathsf{\mathcal{X}})\in {{\mathbb{C}}^{p\times p\times L}}$ $p\times p$ s 设置为$p/2$ . 相似性权重${{w}_{i,j}}$ $\mathsf{\mathcal{M}}$
(7) ${{w}_{i,j}}=\exp \left( {-\left\| {{\mathbf{Q}}_{{{\mathbf{q}}_{i}}}}(\mathbf{\hat{M}})-{{\mathbf{Q}}_{{{\mathbf{q}}_{j}}}}(\mathbf{\hat{M}}) \right\|_{F}^{2}}/{{{\sigma }^{2}}}\; \right)$
其中,$\sigma $ $\hat{M}$
通过引入图拉普拉斯算子$\mathbf{L}$ [24 26] ,流形结构正则化项可重写为矩阵运算形式:
(8) ${{\mathsf{\mathcal{J}}}_{\text{MS}}}(\mathsf{\mathcal{X}})=\text{Tr}\left[ \mathbf{Q}(\mathsf{\mathcal{X}})\mathbf{LQ}{{(\mathsf{\mathcal{X}})}^{H}} \right]$
其中,$\text{Tr}(\cdot )$ $\mathbf{Q}(\mathsf{\mathcal{X}})$ $\mathsf{\mathcal{X}}$ ${{\mathbf{Q}}_{\mathbf{q}}}(\mathsf{\mathcal{X}})$ . 图拉普拉斯算子$\mathbf{L}$ [24 ,33 ] 定义为:
(9) $\mathbf{L}=\mathbf{D}-\mathbf{W}$
其中,$\mathbf{D}$ ${{\mathbf{D}}_{i,i}}=\sum{{{w}_{i,j}}}$ $\mathbf{W}$
(10) $\mathbf{L}=\left[ \begin{matrix} {{w}_{1,2}}+{{w}_{1,3}} & -{{w}_{1,2}} & -{{w}_{1,3}} \\ -{{w}_{1,2}} & {{w}_{1,2}}+{{w}_{2,3}} & -{{w}_{2,3}} \\ -{{w}_{1,3}} & -{{w}_{2,3}} & {{w}_{1,3}}+{{w}_{2,3}} \\\end{matrix} \right]$
2.2 基于流形结构正则化与局部低秩先验的(Manifold Structured Data and Locally Low-rank,MS-LLR)重建框架
流形结构正则化能够有效捕捉MRF数据中的非局部和非线性冗余信息,但对数据块内部的先验信息缺乏考量.本文进一步引入了局部低秩先验,充分利用数据块内的相关信息以进一步提升重建性能.所提出的MRF数据重建方法,简记为MS-LLR,可以表述为如下凸优化问题:
(11) ${{\min }_{\mathsf{\mathcal{X}}\in \mathsf{\mathcal{S}}}}\frac{1}{2}\left\| \mathsf{\mathcal{A}\mathcal{X}}-\mathbf{b} \right\|_{F}^{2}+{{\lambda }_{1}}{{\mathsf{\mathcal{J}}}_{\text{MS}}}(\mathsf{\mathcal{X}})+{{\lambda }_{2}}{{\mathsf{\mathcal{J}}}_{\text{LLR}}}(\mathsf{\mathcal{X}})$
其中,${{\lambda }_{1}}$ ${{\lambda }_{2}}$ ${{\mathsf{\mathcal{J}}}_{\text{MS}}}(\mathsf{\mathcal{X}})$ ${{\mathsf{\mathcal{J}}}_{\text{LLR}}}(\mathsf{\mathcal{X}})$
(12) ${{\mathsf{\mathcal{J}}}_{\text{LLR}}}(\mathsf{\mathcal{X}})=\sum\limits_{i}{{{\left\| {{\mathbf{Q}}_{{{\mathbf{q}}_{i}}}}(\mathsf{\mathcal{X}}) \right\|}_{*}}}$
其中,${{\left\| \cdot \right\|}_{*}}$
根据(8)和(12)式,所提出的重建方法的优化问题可以具体表述为:
(13) ${{\min }_{\mathsf{\mathcal{X}}\in \mathsf{\mathcal{S}}}}\frac{1}{2}\left\| \mathsf{\mathcal{A}\mathcal{X}}-\mathbf{b} \right\|_{F}^{2}+{{\lambda }_{1}}\text{Tr}\left[ \mathbf{Q}(\mathsf{\mathcal{X}})\mathbf{LQ}{{(\mathsf{\mathcal{X}})}^{H}} \right]+{{\lambda }_{2}}\sum\limits_{i}{{{\left\| {{\mathbf{Q}}_{{{\mathbf{q}}_{i}}}}(\mathsf{\mathcal{X}}) \right\|}_{*}}}$
2.3 优化算法
问题(13)可采用增量次梯度-邻近点方法[34 ] 来迭代求解,第n 次迭代涉及求解以下两个子问题:
(14) ${{\mathbf{Z}}^{n}}={{\mathsf{\mathcal{P}}}_{\mathsf{\mathcal{S}}}}\left\{ {{\mathsf{\mathcal{X}}}^{n}}-\mu \left[ {{\mathsf{\mathcal{A}}}^{*}}(\mathsf{\mathcal{A}}{{\mathsf{\mathcal{X}}}^{n}}-\mathbf{b})+{{\lambda }_{1}}{{\mathbf{Q}}^{*}}(\mathbf{Q}({{\mathsf{\mathcal{X}}}^{n}}){{\mathbf{L}}^{n}}) \right] \right\}$
(15) ${{\mathsf{\mathcal{X}}}^{n+1}}=\arg {{\min }_{\mathsf{\mathcal{X}}}}{{\lambda }_{2}}\sum\limits_{i}{{{\left\| {{\mathbf{Q}}_{{{\mathbf{q}}_{i}}}}(\mathsf{\mathcal{X}}) \right\|}_{*}}}+\frac{1}{2\mu }\left\| \mathsf{\mathcal{X}}-{{\mathbf{Z}}^{n}} \right\|_{F}^{2}$
其中,${{\mathsf{\mathcal{A}}}^{*}}$ ${{\mathbf{Q}}^{*}}$ $\mathsf{\mathcal{A}}$ $\mathbf{Q}$ ${{\mathsf{\mathcal{P}}}_{\mathsf{\mathcal{S}}}}(\cdot )$ $\mathsf{\mathcal{S}}$ μ 是步长,取值大于0.${{Z}^{n}}$
(16) ${{\mathsf{\mathcal{P}}}_{\mathsf{\mathcal{S}}}}(\mathbf{X})=\mathbf{X}{{\mathbf{d}}^{\dagger }}\mathbf{d}$
其中,$\mathbf{d}$ $\mathsf{\mathcal{S}}$ $\mathbf{D}$ [11 ] .
子问题(15)无法解析求解,此处引入变量分裂和交替最小化法来高效求解.通过变量分裂,子问题(15)可重写为:
(17) ${{\min }_{\mathsf{\mathcal{X}}}}{{\lambda }_{2}}\sum\limits_{i}{{{\left\| {{\mathbf{P}}_{{{\mathbf{q}}_{i}}}} \right\|}_{*}}}+\frac{1}{2\mu }\left\| \mathsf{\mathcal{X}}-{{\mathbf{Z}}^{n}} \right\|_{2}^{2}\ \ \ s.t.\ \ \ {{\mathbf{P}}_{{{\mathbf{q}}_{i}}}}={{\mathbf{Q}}_{{{\mathbf{q}}_{i}}}}(\mathsf{\mathcal{X}})$
其中,${{\mathbf{P}}_{{{\mathbf{q}}_{i}}}}$
(18) ${{\min }_{\mathsf{\mathcal{X}}}}{{\lambda }_{2}}\sum\limits_{i}{{{\left\| {{\mathbf{P}}_{{{\mathbf{q}}_{i}}}} \right\|}_{*}}}+\frac{1}{2\mu }\left\| \mathsf{\mathcal{X}}-{{\mathbf{Z}}^{n}} \right\|_{2}^{2}+\frac{{{\lambda }_{2}}\beta }{2}\sum\limits_{i}{\left\| {{\mathbf{P}}_{{{\mathbf{q}}_{i}}}}-{{\mathbf{Q}}_{{{\mathbf{q}}_{i}}}}\left( \mathsf{\mathcal{X}} \right) \right\|_{2}^{2}}$
其中,$\beta $
(19) ${{\min }_{{{\mathbf{P}}_{{{\mathbf{q}}_{i}}}}}}\sum\limits_{i}{\left( {{\left\| {{\mathbf{P}}_{{{\mathbf{q}}_{i}}}} \right\|}_{*}}+\frac{\beta }{2}\left\| {{\mathbf{P}}_{{{\mathbf{q}}_{i}}}}-{{\mathbf{Q}}_{{{\mathbf{q}}_{i}}}}(\mathsf{\mathcal{X}}) \right\|_{2}^{2} \right)}$
(20) ${{\min }_{\mathsf{\mathcal{X}}}}\frac{1}{2\mu }\left\| \mathsf{\mathcal{X}}-{{\mathbf{Z}}^{n}} \right\|_{2}^{2}+\frac{{{\lambda }_{2}}\beta }{2}\sum\limits_{i}{\left\| {{\mathbf{P}}_{{{\mathbf{q}}_{i}}}}-{{\mathbf{Q}}_{{{\mathbf{q}}_{i}}}}\left( \mathsf{\mathcal{X}} \right) \right\|_{2}^{2}}$
子问题(19)可通过奇异值阈值(SVT)算法对每个局部数据块求解,在第n次迭代时:
(21) $\mathrm{P}_{{{\mathbf{q}}_{i}}}^{n+1}=\sum{\text{m}}\text{ax}({{\sigma }_{i}}-\frac{1}{\beta },0){{\mathbf{U}}_{i}}\mathbf{V}_{i}^{H}$
其中,特征向量和特征值矩阵可以通过奇异值分解求得${{\mathbf{Q}}_{{{\mathbf{q}}_{i}}}}({{\mathsf{\mathcal{X}}}^{n}})=\sum{{{\sigma }_{i}}}{{\mathbf{U}}_{i}}\mathbf{V}_{i}^{H}$ ${{\mathbf{U}}_{i}}$ $\mathbf{V}_{i}^{{}}$ ${{\sigma }_{i}}$ i 个特征值.
子问题(20)是一个二次优化问题,可通过以下解析形式求解:
(22) ${{\mathsf{\mathcal{X}}}^{n+1}}=\frac{1}{1+\mu {{\lambda }_{2}}\beta }\left[ {{\mathbf{Z}}^{n}}+\mu {{\lambda }_{2}}\beta {{\mathbf{Q}}^{*}}({{\mathbf{P}}^{n+1}}) \right]$
其中,$\mathbf{P}$ ${{\mathbf{P}}_{{{\mathbf{q}}_{i}}}}$ .
2.4 应用细节
本文所提出的方法在一台配备英特尔至强(Intel Xeon)中央处理器(CPU)和英伟达(Nvidia)Quadro GV100图形处理器(GPU)的Linux工作站上进行实现与实验验证.为了更精细地平衡正则化项,流形正则化项的惩罚参数${{\lambda }_{1}}$ $\mathbf{L}$ $\lambda _{1}^{n}=\lambda _{1}^{0}\times \text{max}({{\mathbf{L}}^{n}})$ $\lambda _{1}^{0}$ $\mu =1$ ${{\lambda }_{2}}=0.1$ $\beta =1/5$ . 算法最大迭代次数设置为50.算法中还引入一个由GPU加速的非均匀快速傅里叶变换(NUFFT)库[35 ] ,以在非笛卡尔采样场景中提升所提方法的重建效率.
3 实验结果
为验证所提出方法的有效性,本文在模拟数据和体内实采数据上分别开展了重建实验,并与几种当前最先进(SOTA)的方法进行了比较,这些方法包括:基于迭代投影的重建方法(BLIP)[6 ] 、基于模型的迭代重建方法(MBIR)[7 ] 、基于低秩的快速重建方法(FLOR)[8 ] 、基于结构低秩与子空间投影的重建方法(SL-SP)[11 ] 以及基于低秩约束与深度生成先验的重建方法(DG-LR)[36 ] .此外,为了进一步验证所提出方法的有效性,实验中还纳入了仅使用流形结构正则化项(MS)和仅使用局部低秩约束(LLR)的重建结果作为消融实验(Ablation Study).所有涉及方法的实验参数均经过调优,以确保各方法在最佳性能下进行公平对比.
实验中,基于扩展相图(extended phase graph,EPG)仿真[37 ] 构建指纹字典,参数离散化方案如下:(1)纵向弛豫时间T 1 的取值范围为[100, 5 000] ms,其中在[100, 2 000] ms范围内的增量为20 ms,在 [2 300, 5 000] ms范围内的增量为300 ms;(2)横向弛豫时间T 2 的取值范围为[20, 1 900] ms,其中在[20 ,100] ms范围内的增量为5 ms,在[110,200] ms范围内的增量为10 ms,在[300, 1 900] ms范围内的增量为200 ms.通过剔除T 1 值小于T 2 值的组合,上述设置下指纹字典共涵盖了3 336种组织指纹响应信号.
所有实验均采用稳态进动快速成像(Fast Imaging with Steady State Precession,FISP)[36 ] 脉冲序列进行数据采集,翻转角(FA)和重复时间(TR)模式如图3 中的(a)、(b)子图所示,回波时间(TE)固定为2.94 ms. 实验中采用了三种不同的采样轨迹,如图3 中的(c)、(d)、(e)子图所示,这些采样轨迹包括螺旋采样轨迹(Spiral)、径向采样轨迹(Radial)和变密度螺旋采样轨迹(Variable density spiral,Vds-spiral),全面验证所提方法在多种数据采集条件下的鲁棒性和适用性.
图3
图3
(a)和(b)分别表示实验中使用的翻转角和重复时间模式. (c)、(d)、(e)分别展示了实验中在一个重复时间内使用的螺旋欠采样轨迹、伪径向笛卡尔采样掩模以及变密度螺旋欠采样轨迹
Fig. 3
(a) and (b) are the flip angles and repetition time patterns that were used in the experiment. (c), (d), (e) shows the spiral undersampling trajectory, pseudo radial Cartesian sampling mask, and the variable density spiral undersampling trajectory, respectively, used in one repetition time in the experiments
实验中采用了两个性能评估指标来定量评估所提出方法的性能,分别是信噪比(SNR)和归一化均方误差(NMSE).信噪比(SNR)用来衡量重建的MRF数据的质量,其定义如下:
(23) $\text{SNR = }-\text{10}{{\log }_{\text{10}}}\left( {\left\| \mathsf{\mathcal{X}}-\mathsf{\hat{\mathcal{X}}} \right\|_{F}^{\text{2}}}/{\left\| \mathsf{\mathcal{X}} \right\|_{F}^{\text{2}}}\; \right)$
其中,$\mathsf{\mathcal{X}}$ $\mathsf{\hat{\mathcal{X}}}$
归一化均方误差(NMSE)用于衡量重建的参数图$\mathrm{\hat{M}}$
(24) $\text{NMSE}={{{\left\| {{{\hat{m}}}_{i}}-{{m}_{i}} \right\|}^{2}}}/{{{\left\| {{m}_{i}} \right\|}^{2}}}\;$
其中,${{m}_{i}}$ ${{\hat{m}}_{i}}$ i 处体素的真实参数值和重建参数值.
3.1 仿真实验
仿真实验参考了先前主流研究[8 ,11 ] 的实验设置,利用已知的定量参数图对每种算法的重建性能进行了评估.组织定量参数图的真值由三个已知的定量参数矩阵组成,其参数范围分别为T 1 $\in $ T 2 $\in $ $\in $ k 空间系数,中心区域尺寸为20 cm,视场(FOV)为24 cm[详见图3(e) ],对应的采样率约为5%.为了模拟含噪欠采样的测量数据,在k 空间数据中添加了标准差为0.5的复高斯白噪声,对应的信噪比为29 dB.
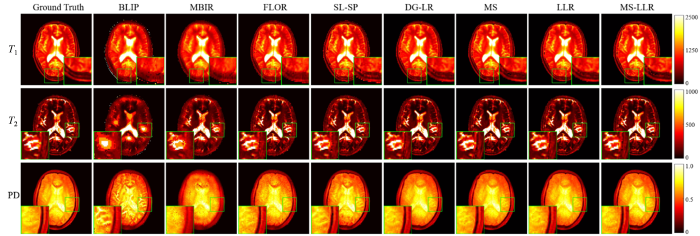
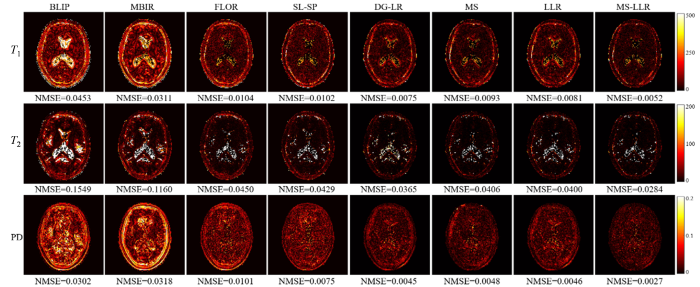
图4 展示了使用5%含噪欠采样数据(采集长度为500)的重建结果.第一列显示了参数图的真值图,而 第2至第9列分别对应使用BLIP、MBIR、FLOR、SL-SP、DG-LR、MS、LLR 和所提出的MS-LLR方法重建的参数图,其中PD参数图经过归一化处理以便于显示.图5 显示了与图4 相对应的重建误差图,报告了各个方法重建的参数图与真值间的误差.从结果可以看出,BLIP和MBIR方法由于未能充分利用MRF数据的特性,表现出明显的模糊和重建偏差,并受到噪声和欠采样伪影的显著影响.相比之下,通过利用MRF数据的相关性先验(如低秩性和结构化低秩性),FLOR和SL-SP方法能够提供改进的重建结果,并恢复更多的细节信息.仅使用流形结构正则化项(MS)或局部低秩约束(LLR)的方法在性能上略优于现有的FLOR、SL-SP等方法,但提升有限.而通过结合流形结构正则化先验与局部低秩约束,所提出的MS-LLR方法实现了最高精度的重建参数图.这一结果充分验证了所提出方法在降低欠采样伪影、提高定量成像精度方面的有效性.
图4
图4
使用5%含噪欠采样数据(采集长度为500)重建的定量参数图
Fig. 4
Reconstructed parameter maps from 5% noisy undersampled measurements with the acquisition length of L =500
图5
图5
重建参数图与真值图之间的误差图,与图4相对应
Fig. 5
Error maps between the reconstructed parameter maps and the reference maps corresponding to Fig. 4
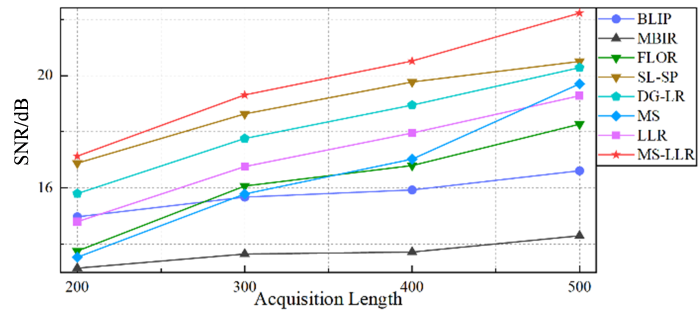
此外,实验还研究了不同采集长度对各算法重建性能的影响.图6 绘制了各方法在不同采集长度的含噪欠采样数据下,重建MRF数据的信噪比(SNR)变化曲线.表2 则详细报告了不同采集长度下重建定量参数图的归一化均方误差(NMSE).实验结果表明,随着采集数据长度的增加,各方法的性能均有所提升.然而,所提出的MS-LLR方法在所有采集长度下均表现出最优的重建性能.具体而言,与现有最佳方法(SL-SP)相比,MS-LLR方法在数据长度为500时重建的MRF数据的信噪比提升了约2 dB,充分验证了该方法在提高重建质量方面的卓越性能.进一步分析发现,单独采用流形正则化先验的MS方法在短时采集数据中重建效果相对较差,但随着数据长度的增加,其性能呈现快速提升趋势.这可能由于其性能高度依赖于流形结构的估计精度,而短时数据难以准确捕捉复杂的流形特征.相比之下,基于局部低秩约束的重建方法在短时数据条件下表现出更强的约束能力.通过将这两种机制有机结合,MS-LLR方法成功整合了流形正则化的全局特征学习与局部低秩约束的细节保持优势,从而在不同数据长度条件下均能获得最优重建效果.
图6
图6
不同方法在使用不同采集长度L 和5%含噪欠采样数据时重建的时空矩阵$\mathsf{\mathcal{X}}$
Fig. 6
The SNRs (dB) of the reconstructed $\mathsf{\mathcal{X}}$ L and 5% noisy undersampled data
3.2 实采数据实验
本节使用在一台3T西门子Prisma磁共振扫描仪上采集的健康人脑实采数据进行实验.实验采用16通道头线圈以及螺旋采样轨迹[见图3(c) ],每帧采集2 880个采样点,对应的采样率约为6%,其他主要成像参数包括视场(FOV)220×220 mm2 ,层厚5 mm.由于实采数据无法获取全采样的真值,实验中遵循先前研究[11 ] 的策略,将原始MRF成像方法在采集长度为1 000时估计的定量参数图作为参考值.
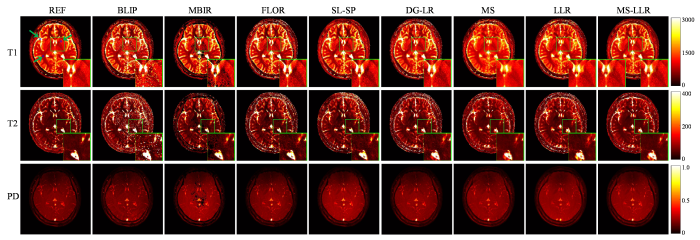
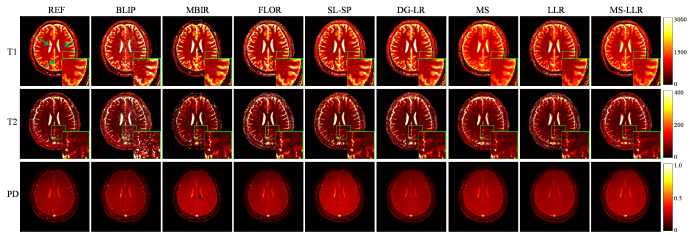
图7 和图8 分别展示了不同方法在采集长度为500时对两名健康志愿者各使用一组实采数据重建的参数图.从结果可以看出,BLIP和MBIR方法能够恢复更锐利的图像,但引入了较多类似噪声的孤立点偏差.FLOR和SL-SP方法通过提供更精确的参数估计展示了改进的重建效果.相比之下,所提出的MS-LLR算法在重建参数图中提供了最清晰的组织细节,表现出最佳的重建质量.为进一步评估所提出方法的性能,将图7 和图8 中蓝色框(第1行第1列箭头所指)标注区域内测量的几种典型脑组织的T 1 和T 2 定量成像值与文献报告的值[38 ] 进行了定性比较,比较结果见表3 和表4 .这些典型脑组织包括脑灰质(Gray Matter, GM)、脑白质(White Matter, WM)和脑脊液(Cerebrospinal Fluid, CSF).结果显示,所提出的MS-LLR方法提供了最稳定的参数估计,其估计值与参考值及文献[38 ] 中的报告值最为一致,进一步验证了该方法在实际应用中的可靠性和准确性.
图7
图7
使用实际采集自一名健康志愿者的欠采样数据(采集长度为500)重建的定量参数图
Fig. 7
Reconstructed parameter maps from in vivo undersampled measurements with the acquisition length of L =500 collected from a healthy volunteer
图8
图8
使用实际采集自另一名健康志愿者的欠采样数据(采集长度为500)重建的定量参数图
Fig. 8
Reconstructed parameter maps from in vivo undersampled measurements with the acquisition length of L =500 collected from a healthy volunteer
4 分析与讨论
4.1 超参数设置
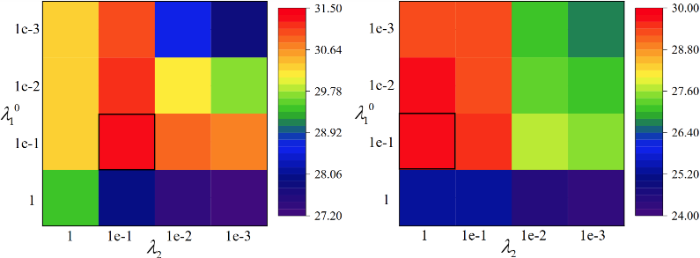
图9 展示了不同正则项超参数设置组合下算法的重建性能,其中最优参数组合以黑色方框突出显示.实验中分别使用了螺旋采样轨迹[图3(c) ]和径向采样轨迹[图3(d) ],数据采集长度为500.从结果可以看出,所提出方法在不同的采样轨迹下表现出良好的参数鲁棒性,两种轨迹的最优参数设置高度一致,$\lambda _{1}^{0}$ ${{\lambda }_{2}}$ ${{\lambda }_{2}}$
图9
图9
不同超参数组合下重建MRF数据的信噪比. 左图:径向采样轨迹,右图:螺旋采样轨迹
Fig. 9
SNR values of the reconstructed MRF data as functions of the parameters. Left: radial Cartesian trajectories; right: spiral trajectories
表5 给出了不同块尺寸下算法重建定量参数的归一化均方误差.该实验同样分别使用了螺旋采样轨迹[图3(c) ]和径向采样轨迹[图3(d) ]两种欠采样轨迹,数据采集长度设置为500.实验结果表明,所提出方法的重建精度对块尺寸的设置并不敏感,不同块尺寸下的重建误差差距较小.考虑到较大尺寸的局部块能够有效降低计算开销,本文建议将局部块尺寸设置为11×11.
4.2 不同采样轨迹下算法性能
表6 为所提出方法在不同采样轨迹下与其他方法的重建性能对比.实验中采用了3种欠采样轨迹:螺旋采样轨迹(Spiral)、变密度螺旋采样轨迹(Vds-spiral)以及径向采样轨迹(Radial).数据采集长度为500,采样率约为5%.实验结果表明,所提出方法在所有采样轨迹下均能够提供最优的重建结果,充分验证了该方法的有效性及其在不同采样条件下的高泛化能力.此外,实验结果还显示,SL-SP方法在经向采样轨迹下T 1 参数精度最高,这也表明了低频信息足够丰富时,现有的复杂数据模型的方法也能够取得较好的效果,但其计算复杂度要远远高于本文方法.
4.3 指纹流形与参数流形拓扑一致性分析
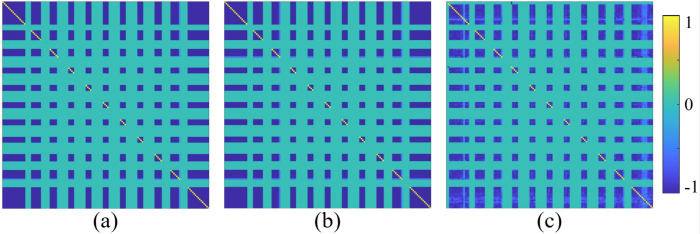
我们通过实验验证了MRF数据与其对应的定量参数图之间的嵌入关系,进而验证了指纹流形与参数流形拓扑一致性的假设.具体而言,我们基于一组MRF数据及其对应的定量参数图估计了各自的拉普拉斯矩阵L ,并通过可视化展示了其结构特性,如图10 所示.图10 分别展示了三种情况下的拉普拉斯矩阵估计结果,图10(a) 使用全采样MRF数据,图10(b) 使用与之对应的定量参数图,图10(c) 使用所提出方法从欠采样数据重建的MRF数据.实验结果显示,由全采样MRF数据和其对应定量参数图估计的拉普拉斯矩阵L 表现出高度相似性,两者的相关系数高达0.997 6.这一结果有力地支持了指纹流形与参数流形在拓扑结构上具有一致性的假设.对于欠采样MRF数据,由于欠采样伪影的干扰,其估计的拉普拉斯矩阵在细节上表现出一定的偏差.然而,总体来看,该矩阵仍然能够较好地恢复MRF数据的潜在流形结构.这一现象不仅反映了欠采样对数据拓扑结构的影响,同时也验证了所提出方法在重建过程中对潜在流形结构的有效保持能力.
图10
图10
基于拉普拉斯矩阵的指纹流形与参数流形一致性分析. 拉普拉斯矩阵L 可视化图,计算自:(a)全采样的MRF数据,(b)真值参数图,(c)由欠采样数据重建的MRF数据
Fig. 10
Analysis of consistency between fingerprint manifold and parameter manifold based on Laplacian matrix. Visualization of the Laplacian matrix L
4.4 计算开销
所提出的方法通过共享的块提取算子,同时利用了流形结构先验和局部低秩先验.这一设计不仅强化了对数据结构先验信息的利用,还显著降低了算法的计算复杂度.此外,为了进一步提升非笛卡尔采样场景下的计算效率,本文采用了基于GPU加速的非均匀快速傅里叶变换库[35 ] .表7 展示了不同方法在非笛卡尔采样模式下的平均计算时间,实验中采用了变密度螺旋轨迹[图3(e) ],数据采集长度为500.结果表明,与现有的最先进方法(SOTA)相比,所提出方法显著减少了重建耗时.在相同实验场景下,所提出方法的重建耗时仅为其他方法的8.8%~25.0%,充分体现了其在计算效率上的优越性.
5 结论
本文提出了一种结合流形结构正则化和局部低秩约束的新型MRF重建方法,该方法首次将流形正则化引入MRF重建领域,并揭示了指纹流形与参数流形之间内在拓扑结构的一致性.通过挖掘高维MRF数据中的非局部冗余信息和非线性特性,并结合高维数据的低维流形表征,所提出的方法在重建性能和计算效率方面相较于现有最先进方法均表现出显著提升.此外,该方法对噪声和欠采样伪影具有高度抑制能力,并在复杂场景下展现出优异的鲁棒性.通过对高维MRF数据进行低维流形结构表征,所提出方法显著降低了后处理阶段的计算开销,为MRF成像领域引入了一种全新的应用范式,对于推动MRF技术在临床实践中的普惠应用奠定了基础,具有科学意义和实际价值.未来的研究方向可以进一步聚焦于以下方面: (1)在更复杂的成像场景中优化算法的计算效率和泛化能力;(2)探索深度学习与流形正则化相结合的混合框架,以进一步提升重建性能,满足更广泛的临床需求.
利益冲突
参考文献
View Option
[1]
MA D GULANI V SEIBERLICH N , et al . Magnetic resonance fingerprinting
[J]. Nature , 2013 , 495 (7440 ): 187 -192 .
[本文引用: 3]
[2]
CHEN Y LU L ZHU T , et al . Technical overview of magnetic resonance fingerprinting and its applications in radiation therapy
[J]. Med Phys , 2022 , 49 (4 ): 2846 -2860 .
[本文引用: 1]
[3]
DENG W LI X H . Research progress of cardiac magnetic resonance fingerprint technology
[J]. International Journal Of Medical Radiology , 2022 , 45 (2 ): 189 -191 ;204.
[本文引用: 1]
邓炜 , 李小虎 . 心脏磁共振指纹技术研究进展
[J]. 国际医学放射学杂志 , 2022 , 45 (2 ): 189 -191 ,204.
[本文引用: 1]
[4]
LENG Y J WU Q W, LI Y X, et al Quantitative measurement of brain tissue parameters based on magnetic resonance fingerprinting and its preliminary application in brain diseases
[J], Chinese Journal of Clinical Neurosciences , 2020 , 28 (5 ): 579 -583 .
[本文引用: 1]
冷一峻 , 吴秋雯 , 李郁欣 , 等 . 基于磁共振指纹技术的脑组织参数定量检测及在脑疾病中的初步应用
[J]. 中国临床神经科学 , 2020 , 28 (5 ): 579 -583 .
[本文引用: 1]
[5]
TIPPAREDDY C ZHAO W SUNSHINE J L , et al . Magnetic resonance fingerprinting: an overview
[J]. Eur J Nucl Med Mol I , 2021 , 48 (13 ): 4189 -4200 .
[本文引用: 2]
[6]
DAVIES M PUY G VANDERGHEYNST P , et al . A compressed sensing framework for magnetic resonance fingerprinting
[J]. SIAM J Imaging Sci , 2014 , 7 (4 ): 2623 -2656 .
[本文引用: 6]
[7]
ZHAO B SETSOMPOP K YE H , et al . Maximum likelihood reconstruction for magnetic resonance fingerprinting
[J]. IEEE T Med Imaging , 2016 , 35 (8 ): 1812 -1823 .
DOI:10.1109/TMI.2016.2531640
PMID:26915119
[本文引用: 2]
This paper introduces a statistical estimation framework for magnetic resonance (MR) fingerprinting, a recently proposed quantitative imaging paradigm. Within this framework, we present a maximum likelihood (ML) formalism to estimate multiple MR tissue parameter maps directly from highly undersampled, noisy k-space data. A novel algorithm, based on variable splitting, the alternating direction method of multipliers, and the variable projection method, is developed to solve the resulting optimization problem. Representative results from both simulations and in vivo experiments demonstrate that the proposed approach yields significantly improved accuracy in parameter estimation, compared to the conventional MR fingerprinting reconstruction. Moreover, the proposed framework provides new theoretical insights into the conventional approach. We show analytically that the conventional approach is an approximation to the ML reconstruction; more precisely, it is exactly equivalent to the first iteration of the proposed algorithm for the ML reconstruction, provided that a gridding reconstruction is used as an initialization.
[8]
MAZOR G WEIZMAN L TAL A , et al . Low-rank magnetic resonance fingerprinting
[J]. Med Phys , 2018 , 45 (9 ): 4066 -4084 .
[本文引用: 3]
[9]
ZHAO B SETSOMPOP K ADALSTEINSSON E , et al . Improved magnetic resonance fingerprinting reconstruction with low-rank and sssubspace modeling
[J]. Magn Reson Med , 2018 , 79 (2 ): 933 -942 .
[本文引用: 1]
[10]
LIMA DA CRUZ G BUSTIN A JAUBERT O , et al . Sparsity and locally low rank regularization for MR fingerprinting
[J]. Magn Reson Med , 2019 , 81 (6 ): 3530 -3543 .
DOI:10.1002/mrm.27665
PMID:30720209
[本文引用: 1]
Develop a sparse and locally low rank (LLR) regularized reconstruction to accelerate MR fingerprinting (MRF).Recent works have introduced low rank reconstructions to MRF, based on temporal compression operators learned from the MRF dictionary. In other MR applications, LLR regularization has been introduced to exploit temporal redundancy in local regions of the image. Here, we propose to include spatial sparsity and LLR regularization terms in the MRF reconstruction. This approach, so called SLLR-MRF, further reduces aliasing in the time-point images and enables higher acceleration factors. The proposed approach was evaluated in simulations, T /T phantom acquisition, and in vivo brain acquisitions in 5 healthy subjects with different undersampling factors. Acceleration was also used in vivo to enable acquisitions with higher in-plane spatial resolution in comparable scan time.Simulations, phantom, and in vivo results show that low rank MRF reconstructions with high acceleration factors (<875 time-point images, 1 radial spoke per time-point) have residual aliasing artifacts that propagate into the parametric maps. The artifacts are reduced with the proposed SLLR-MRF resulting in considerable improvements in precision, without changes in accuracy. In vivo results show improved parametric maps for the proposed SLLR-MRF, potentially enabling MRF acquisitions with 1 radial spoke per time-point in approximately 2.6 s (~600 time-point images) for 2 × 2 mm and 9.6 s (1750 time-point images) for 1 × 1 mm in-plane resolution.The proposed SLLR-MRF reconstruction further improves parametric map quality compared with low rank MRF, enabling shorter scan times and/or increased spatial resolution.© 2019 The Authors Magnetic Resonance in Medicine published by Wiley Periodicals, Inc. on behalf of International Society for Magnetic Resonance in Medicine.
[11]
HU Y LI P CHEN H , et al . High-quality MR fingerprinting reconstruction using structured low-rank matrix completion and subspace projection
[J]. IEEE T Med Imaging , 2021 , 41 (5 ): 1150 -1164 .
[本文引用: 6]
[12]
NAGTEGAAL M HARTSEMA E KOOLSTRA K , et al . Multicomponent MR fingerprinting reconstruction using joint-sparsity and low-rank constraints
[J]. Magn Reson Med , 2023 , 89 (1 ): 286 -298 .
DOI:10.1002/mrm.29442
PMID:36121015
[本文引用: 1]
To develop an efficient algorithm for multicomponent MR fingerprinting (MC-MRF) reconstructions directly from highly undersampled data without making prior assumptions about tissue relaxation times and expected number of tissues.The proposed method reconstructs MC-MRF maps from highly undersampled data by iteratively applying a joint-sparsity constraint to the estimated tissue components. Intermediate component maps are obtained by a low-rank multicomponent alternating direction method of multipliers (MC-ADMM) including the non-negativity of tissue weights as an extra regularization term. Over iterations, the used dictionary compression is adjusted. The proposed method (k-SPIJN) is compared with a two-step approach in which image reconstruction and multicomponent estimations are performed sequentially and tested in numerical simulations and in vivo by applying different undersampling factors in eight healthy volunteers. In the latter case, fully sampled data serves as the reference.The proposed method shows improved precision and accuracy in simulations compared with a state-of-art sequential approach. Obtained in vivo magnetization fraction maps for different tissue types show reduced systematic errors and reduced noise-like effects. Root mean square errors in estimated magnetization fraction maps significantly reduce from 13.0% 5.8% with the conventional, two-step approach to 9.6% 3.9% and 9.6% 3.2% with the proposed MC-ADMM and k-SPIJN methods, respectively. Mean standard deviation in homogeneous white matter regions reduced significantly from 8.6% to 2.9% (two step vs. k-SPIJN).The proposed MC-ADMM and k-SPIJN reconstruction methods estimate MC-MRF maps from highly undersampled data resulting in improved image quality compared with the existing method.© 2022 The Authors. Magnetic Resonance in Medicine published by Wiley Periodicals LLC on behalf of International Society for Magnetic Resonance in Medicine.
[13]
MCGIVNEY D F PIERRE E MA D , et al . SVD compression for magnetic resonance fingerprinting in the time domain
[J]. IEEE T Med Imaging , 2014 , 33 (12 ): 2311 -2322 .
DOI:10.1109/TMI.2014.2337321
PMID:25029380
[本文引用: 1]
Magnetic resonance (MR) fingerprinting is a technique for acquiring and processing MR data that simultaneously provides quantitative maps of different tissue parameters through a pattern recognition algorithm. A predefined dictionary models the possible signal evolutions simulated using the Bloch equations with different combinations of various MR parameters and pattern recognition is completed by computing the inner product between the observed signal and each of the predicted signals within the dictionary. Though this matching algorithm has been shown to accurately predict the MR parameters of interest, one desires a more efficient method to obtain the quantitative images. We propose to compress the dictionary using the singular value decomposition, which will provide a low-rank approximation. By compressing the size of the dictionary in the time domain, we are able to speed up the pattern recognition algorithm, by a factor of between 3.4-4.8, without sacrificing the high signal-to-noise ratio of the original scheme presented previously.
[14]
YANG M MA D JIANG Y , et al . Low rank approximation methods for MR fingerprinting with large scale dictionaries
[J]. Magn Reson Med , 2018 , 79 (4 ): 2392 -2400 .
DOI:10.1002/mrm.26867
PMID:28804918
[本文引用: 1]
This work proposes new low rank approximation approaches with significant memory savings for large scale MR fingerprinting (MRF) problems.We introduce a compressed MRF with randomized singular value decomposition method to significantly reduce the memory requirement for calculating a low rank approximation of large sized MRF dictionaries. We further relax this requirement by exploiting the structures of MRF dictionaries in the randomized singular value decomposition space and fitting them to low-degree polynomials to generate high resolution MRF parameter maps. In vivo 1.5T and 3T brain scan data are used to validate the approaches.T, T, and off-resonance maps are in good agreement with that of the standard MRF approach. Moreover, the memory savings is up to 1000 times for the MRF-fast imaging with steady-state precession sequence and more than 15 times for the MRF-balanced, steady-state free precession sequence.The proposed compressed MRF with randomized singular value decomposition and dictionary fitting methods are memory efficient low rank approximation methods, which can benefit the usage of MRF in clinical settings. They also have great potentials in large scale MRF problems, such as problems considering multi-component MRF parameters or high resolution in the parameter space. Magn Reson Med 79:2392-2400, 2018. © 2017 International Society for Magnetic Resonance in Medicine.© 2017 International Society for Magnetic Resonance in Medicine.
[15]
COHEN O ZHU B ROSEN M S . MR fingerprinting deep reconstruction network (DRONE)
[J]. Magn Reson Med , 2018 , 80 (3 ): 885 -894 .
DOI:10.1002/mrm.27198
PMID:29624736
[本文引用: 1]
[16]
OKSUZ I CRUZ G CLOUGH J , et al . Magnetic resonance fingerprinting using recurrent neural networks
[C]// 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019). IEEE , 2019 : 1537 -1540 .
[本文引用: 1]
[17]
FANG Z CHEN Y LIU M , et al . Deep learning for fast and spatially constrained tissue quantification from highly accelerated data in magnetic resonance fingerprinting
[J]. IEEE T Med Imaging , 2019 , 38 (10 ): 2364 -2374 .
DOI:10.1109/TMI.2019.2899328
PMID:30762540
[本文引用: 1]
Magnetic resonance fingerprinting (MRF) is a quantitative imaging technique that can simultaneously measure multiple important tissue properties of human body. Although MRF has demonstrated improved scan efficiency as compared to conventional techniques, further acceleration is still desired for translation into routine clinical practice. The purpose of this paper is to accelerate MRF acquisition by developing a new tissue quantification method for MRF that allows accurate quantification with fewer sampling data. Most of the existing approaches use the MRF signal evolution at each individual pixel to estimate tissue properties, without considering the spatial association among neighboring pixels. In this paper, we propose a spatially constrained quantification method that uses the signals at multiple neighboring pixels to better estimate tissue properties at the central pixel. Specifically, we design a unique two-step deep learning model that learns the mapping from the observed signals to the desired properties for tissue quantification, i.e.: 1) with a feature extraction module for reducing the dimension of signals by extracting a low-dimensional feature vector from the high-dimensional signal evolution and 2) a spatially constrained quantification module for exploiting the spatial information from the extracted feature maps to generate the final tissue property map. A corresponding two-step training strategy is developed for network training. The proposed method is tested on highly undersampled MRF data acquired from human brains. Experimental results demonstrate that our method can achieve accurate quantification for T1 and T2 relaxation times by using only 1/4 time points of the original sequence (i.e., four times of acceleration for MRF acquisition).
[18]
SOYAK R NAVRUZ E ERSOY E O , et al . Channel attention networks for robust MR fingerprint matching
[J]. IEEE T Bio-med Eng , 2021 , 69 (4 ): 1398 -1405 .
[本文引用: 1]
[19]
TENENBAUM J B SILVA V LANGFORD J C . A global geometric framework for nonlinear dimensionality reduction
[J]. Science , 2000 , 290 (5500 ): 2319 -2323 .
DOI:10.1126/science.290.5500.2319
PMID:11125149
[本文引用: 3]
Scientists working with large volumes of high-dimensional data, such as global climate patterns, stellar spectra, or human gene distributions, regularly confront the problem of dimensionality reduction: finding meaningful low-dimensional structures hidden in their high-dimensional observations. The human brain confronts the same problem in everyday perception, extracting from its high-dimensional sensory inputs-30,000 auditory nerve fibers or 10(6) optic nerve fibers-a manageably small number of perceptually relevant features. Here we describe an approach to solving dimensionality reduction problems that uses easily measured local metric information to learn the underlying global geometry of a data set. Unlike classical techniques such as principal component analysis (PCA) and multidimensional scaling (MDS), our approach is capable of discovering the nonlinear degrees of freedom that underlie complex natural observations, such as human handwriting or images of a face under different viewing conditions. In contrast to previous algorithms for nonlinear dimensionality reduction, ours efficiently computes a globally optimal solution, and, for an important class of data manifolds, is guaranteed to converge asymptotically to the true structure.
[20]
VAN DER MAATEN L POSTMA E VAN DEN HERIK J . Dimensionality reduction: a comparative
[J]. J Mach Learn Res , 2009 , 10 : 66 -71 .
[本文引用: 1]
[21]
ALJABAR P WOLZ R RUECKERT D . Manifold learning for medical image registration, segmentation, and classification [M]// Machine learning in computer-aided diagnosis : Medical imaging intelligence and analysis , 2012 : 351 -372 .
[本文引用: 1]
[22]
BOUMAL N . An introduction to optimization on smooth manifolds [M]. Cambridge University Press, 2023 .
[本文引用: 1]
[23]
NAKARMI U SLAVAKIS K LYU J , et al . M-MRI: A manifold-based framework to highly accelerated dynamic magnetic resonance imaging
[C]// 2017 IEEE 14th International Symposium on Biomedical Imaging (ISBI 2017). IEEE , 2017 : 19 -22 .
[本文引用: 1]
[24]
PODDAR S JACOB M . Dynamic MRI using smoothness regularization on manifolds (SToRM)
[J]. IEEE T Med Imaging , 2015 , 35 (4 ): 1106 -1115 .
[本文引用: 4]
[25]
PODDAR S MOHSIN Y Q ANSAH D , et al . Manifold recovery using kernel low-rank regularization: Application to dynamic imaging
[J]. IEEE T Comput Imag , 2019 , 5 (3 ): 478 -491 .
DOI:10.1109/tci.2019.2893598
PMID:33768137
We introduce a novel kernel low-rank algorithm to recover free-breathing and ungated dynamic MRI data from highly undersampled measurements. The image frames in the free breathing and ungated dataset are assumed to be points on a bandlimited manifold. We show that the non-linear features of these images satisfy annihilation conditions, which implies that the kernel matrix derived from the dataset is low-rank. We penalize the nuclear norm of the feature matrix to recover the images from highly undersampled measurements. The regularized optimization problem is solved using an iterative reweighted least squares (IRLS) algorithm, which alternates between the update of the Laplacian matrix of the manifold and the recovery of the signals from the noisy measurements. To improve computational efficiency, we use a two step algorithm using navigator measurements. Specifically, the Laplacian matrix is estimated from the navigators using the IRLS scheme, followed by the recovery of the images using a quadratic optimization. We show the relation of this two step algorithm with our recent SToRM approach, thus reconciling SToRM and manifold regularization methods with algorithms that rely on explicit lifting of data to a high dimensional space. The IRLS based estimation of the Laplacian matrix is a systematic and noise-robust alternative to current heuristic strategies based on exponential maps. We also approximate the Laplacian matrix using a few eigen vectors, which results in a fast and memory efficient algorithm. The proposed scheme is demonstrated on several patients with different breathing patterns and cardiac rates.
[26]
MOHSIN Y Q PODDAR S JACOB M . Free-breathing & ungated cardiac MRI using iterative SToRM (i-SToRM)
[J]. IEEE T Med Imaging , 2019 , 38 (10 ): 2303 -2313 .
[本文引用: 1]
[27]
NAKARMI U WANG Y LYU J , et al . A kernel-based low-rank (KLR) model for low-dimensional manifold recovery in highly accelerated dynamic MRI
[J]. IEEE T Med Imaging , 2017 , 36 (11 ): 2297 -2307 .
DOI:10.1109/TMI.2017.2723871
PMID:28692970
[本文引用: 1]
While many low rank and sparsity-based approaches have been developed for accelerated dynamic magnetic resonance imaging (dMRI), they all use low rankness or sparsity in input space, overlooking the intrinsic nonlinear correlation in most dMRI data. In this paper, we propose a kernel-based framework to allow nonlinear manifold models in reconstruction from sub-Nyquist data. Within this framework, many existing algorithms can be extended to kernel framework with nonlinear models. In particular, we have developed a novel algorithm with a kernel-based low-rank model generalizing the conventional low rank formulation. The algorithm consists of manifold learning using kernel, low rank enforcement in feature space, and preimaging with data consistency. Extensive simulation and experiment results show that the proposed method surpasses the conventional low-rank-modeled approaches for dMRI.
[28]
SLAVAKIS K SHETTY G N CANNELLI L , et al . Kernel regression imputation in manifolds via bi-linear modeling: The dynamic-MRI case
[J]. IEEE T Comput Imag , 2022 , 8 : 133 -147 .
[本文引用: 1]
[29]
DJEBRA Y MARIN T HAN P K , et al . Manifold learning via linear tangent space alignment (LTSA) for accelerated dynamic MRI with sparse sampling
[J]. IEEE T Med Imaging , 2022 , 42 (1 ): 158 -169 .
[30]
ARBERET S CHEN X MAILHÉ B , et al . A parallel spatial and Bloch manifold regularized iterative reconstruction method for MR Fingerprinting
[J]. Magn Reson Imaging , 2021 , 82 : 74 -90 .
DOI:10.1016/j.mri.2021.06.009
PMID:34157408
[本文引用: 1]
Magnetic Resonance Fingerprinting (MRF) reconstructs tissue maps based on a sequence of very highly undersampled images. In order to be able to perform MRF reconstruction, state-of-the-art MRF methods rely on priors such as the MR physics (Bloch equations) and might also use some additional low-rank or spatial regularization. However to our knowledge these three regularizations are not applied together in a joint reconstruction. The reason is that it is indeed challenging to incorporate effectively multiple regularizations in a single MRF optimization algorithm. As a result most of these methods are not robust to noise especially when the sequence length is short. In this paper, we propose a family of new methods where spatial and low-rank regularizations, in addition to the Bloch manifold regularization, are applied on the images. We show on digital phantom and NIST phantom scans, as well as volunteer scans that the proposed methods bring significant improvement in the quality of the estimated tissue maps.Copyright © 2021. Published by Elsevier Inc.
[31]
CANNON J W . Shrinking cell-like decompositions of manifolds. Codimension three
[J]. Ann Math , 1979 : 83 -112 .
[本文引用: 1]
[32]
DONG G HINTERMÜLLER M PAPAFITSOROS K . Quantitative magnetic resonance imaging: From fingerprinting to integrated physics-based models
[J]. SIAM J Imaging Sci , 2019 , 12 (2 ): 927 -971 .
[本文引用: 2]
[33]
BELKIN M NIYOGI P . Laplacian eigenmaps for dimensionality reduction and data representation
[J]. Neural Comput , 2003 , 15 (6 ): 1373 -1396 .
[本文引用: 1]
[34]
SRA S NOWOZIN S WRIGHT S J . Optimization for machine learning [M]. Mit Press, 2011 .
[本文引用: 1]
[35]
MUCKLEY M J STERN R MURRELL T , et al . TorchKbNufft: A high-level, hardware-agnostic non-uniform fast Fourier transform
[C]// ISMRM Workshop on Data Sampling & Image Reconstruction . 2020 , 22 .
[本文引用: 2]
[36]
LU H ZHAO B . Accelerated magnetic resonance fingerprinting with low-rank and generative subspace modeling
[C]// 2023 IEEE International Conference on Acoustics, Speech, and Signal Processing Workshops (ICASSPW). IEEE , 2023 : 1 -5 .
[本文引用: 2]
[37]
JIANG Y MA D SEIBERLICH N , et al . MR fingerprinting using fast imaging with steady state precession (FISP) with spiral readout
[J]. Magn Reson Med , 2015 , 74 (6 ): 1621 -1631 .
DOI:10.1002/mrm.25559
PMID:25491018
[本文引用: 1]
This study explores the possibility of using gradient echo-based sequences other than balanced steady-state free precession (bSSFP) in the magnetic resonance fingerprinting (MRF) framework to quantify the relaxation parameters.An MRF method based on a fast imaging with steady-state precession (FISP) sequence structure is presented. A dictionary containing possible signal evolutions with physiological range of T1 and T2 was created using the extended phase graph formalism according to the acquisition parameters. The proposed method was evaluated in a phantom and a human brain. T1, T2, and proton density were quantified directly from the undersampled data by the pattern recognition algorithm.T1 and T2 values from the phantom demonstrate that the results of MRF FISP are in good agreement with the traditional gold-standard methods. T1 and T2 values in brain are within the range of previously reported values.MRF-FISP enables a fast and accurate quantification of the relaxation parameters. It is immune to the banding artifact of bSSFP due to B0 inhomogeneities, which could improve the ability to use MRF for applications beyond brain imaging.© 2014 Wiley Periodicals, Inc.
[38]
BIPIN MEHTA B COPPO S FRANCES MCGIVNEY D , et al . Magnetic resonance fingerprinting: a technical review
[J]. Magn Reson Med , 2019 , 81 (1 ): 25 -46 .
DOI:10.1002/mrm.27403
PMID:30277265
[本文引用: 4]
Multiparametric quantitative imaging is gaining increasing interest due to its widespread advantages in clinical applications. Magnetic resonance fingerprinting is a recently introduced approach of fast multiparametric quantitative imaging. In this article, magnetic resonance fingerprinting acquisition, dictionary generation, reconstruction, and validation are reviewed.© International Society for Magnetic Resonance in Medicine.
Magnetic resonance fingerprinting
3
2013
... 磁共振指纹(Magnetic Resonance Fingerprinting,MRF)成像由凯斯西储大学的Mark Griswold教授团队于2013年首次提出[1 ,2 ] .该技术通过伪随机脉冲激发受检组织,使不同组织生成独特的时变暂态弛豫响应信号,即MRF信号.在频域完成数据采集后,通过逆傅里叶变换重建获得时域信号.同时,基于磁共振信号激发的布洛赫方程,构建一个包含各种人体组织理论MRF信号的字典.通过模式匹配算法,将重建信号与字典中的理论信号进行比对,从而获得多个定量参数,例如自旋-晶格弛豫时间(Spin-lattice Relaxation Time,T 1 )和自旋-自旋弛豫时间(Spin-spin Relaxation Time,T 2 ).这些定量参数能够客观反映组织的生理状态及病理变化,为疾病的早期诊断和疗效评估提供了重要依据.前瞻性临床应用研究表明,MRF成像技术在心脑血管、肿瘤及神经系统等疾病[3 -4 ] 的早期诊断和病理分级方面中展现出显著优势. 然而,为提升信号特异性并加速数据采集,MRF成像通常采用高倍欠采样策略,仅采集少量数据(约2%~8%)[5 ] 用于定量成像. 这导致逆傅里叶变换重建的时域MRF图像中出现严重的混叠伪影,进而降低定量成像的精度. ...
... 其中,$\{{{\eta }_{m}},\ m=1,\cdots,M\}$ $\mathsf{\mathcal{M}}$ $\mathbf{D}$ $\mathbf{D}$ $\mathsf{\mathcal{B}}$ [6 ] 的离散化近似.多参数定量图像可以通过将重建的MRF数据$\mathsf{\hat{\mathcal{X}}}$ [1 ] ,这一过程可以表示为:$\hat{M}={{\Phi }_{\mathbf{D}}}(\mathsf{\hat{\mathcal{X}}})$ $\hat{M}$ ${{\Phi }_{\mathbf{D}}}(\cdot )$ [1 ,11 ] 可以通过预计算的字典$\mathbf{D}$
... [1 ,11 ]可以通过预计算的字典$\mathbf{D}$
Technical overview of magnetic resonance fingerprinting and its applications in radiation therapy
1
2022
... 磁共振指纹(Magnetic Resonance Fingerprinting,MRF)成像由凯斯西储大学的Mark Griswold教授团队于2013年首次提出[1 ,2 ] .该技术通过伪随机脉冲激发受检组织,使不同组织生成独特的时变暂态弛豫响应信号,即MRF信号.在频域完成数据采集后,通过逆傅里叶变换重建获得时域信号.同时,基于磁共振信号激发的布洛赫方程,构建一个包含各种人体组织理论MRF信号的字典.通过模式匹配算法,将重建信号与字典中的理论信号进行比对,从而获得多个定量参数,例如自旋-晶格弛豫时间(Spin-lattice Relaxation Time,T 1 )和自旋-自旋弛豫时间(Spin-spin Relaxation Time,T 2 ).这些定量参数能够客观反映组织的生理状态及病理变化,为疾病的早期诊断和疗效评估提供了重要依据.前瞻性临床应用研究表明,MRF成像技术在心脑血管、肿瘤及神经系统等疾病[3 -4 ] 的早期诊断和病理分级方面中展现出显著优势. 然而,为提升信号特异性并加速数据采集,MRF成像通常采用高倍欠采样策略,仅采集少量数据(约2%~8%)[5 ] 用于定量成像. 这导致逆傅里叶变换重建的时域MRF图像中出现严重的混叠伪影,进而降低定量成像的精度. ...
Research progress of cardiac magnetic resonance fingerprint technology
1
2022
... 磁共振指纹(Magnetic Resonance Fingerprinting,MRF)成像由凯斯西储大学的Mark Griswold教授团队于2013年首次提出[1 ,2 ] .该技术通过伪随机脉冲激发受检组织,使不同组织生成独特的时变暂态弛豫响应信号,即MRF信号.在频域完成数据采集后,通过逆傅里叶变换重建获得时域信号.同时,基于磁共振信号激发的布洛赫方程,构建一个包含各种人体组织理论MRF信号的字典.通过模式匹配算法,将重建信号与字典中的理论信号进行比对,从而获得多个定量参数,例如自旋-晶格弛豫时间(Spin-lattice Relaxation Time,T 1 )和自旋-自旋弛豫时间(Spin-spin Relaxation Time,T 2 ).这些定量参数能够客观反映组织的生理状态及病理变化,为疾病的早期诊断和疗效评估提供了重要依据.前瞻性临床应用研究表明,MRF成像技术在心脑血管、肿瘤及神经系统等疾病[3 -4 ] 的早期诊断和病理分级方面中展现出显著优势. 然而,为提升信号特异性并加速数据采集,MRF成像通常采用高倍欠采样策略,仅采集少量数据(约2%~8%)[5 ] 用于定量成像. 这导致逆傅里叶变换重建的时域MRF图像中出现严重的混叠伪影,进而降低定量成像的精度. ...
心脏磁共振指纹技术研究进展
1
2022
... 磁共振指纹(Magnetic Resonance Fingerprinting,MRF)成像由凯斯西储大学的Mark Griswold教授团队于2013年首次提出[1 ,2 ] .该技术通过伪随机脉冲激发受检组织,使不同组织生成独特的时变暂态弛豫响应信号,即MRF信号.在频域完成数据采集后,通过逆傅里叶变换重建获得时域信号.同时,基于磁共振信号激发的布洛赫方程,构建一个包含各种人体组织理论MRF信号的字典.通过模式匹配算法,将重建信号与字典中的理论信号进行比对,从而获得多个定量参数,例如自旋-晶格弛豫时间(Spin-lattice Relaxation Time,T 1 )和自旋-自旋弛豫时间(Spin-spin Relaxation Time,T 2 ).这些定量参数能够客观反映组织的生理状态及病理变化,为疾病的早期诊断和疗效评估提供了重要依据.前瞻性临床应用研究表明,MRF成像技术在心脑血管、肿瘤及神经系统等疾病[3 -4 ] 的早期诊断和病理分级方面中展现出显著优势. 然而,为提升信号特异性并加速数据采集,MRF成像通常采用高倍欠采样策略,仅采集少量数据(约2%~8%)[5 ] 用于定量成像. 这导致逆傅里叶变换重建的时域MRF图像中出现严重的混叠伪影,进而降低定量成像的精度. ...
Y X, et al Quantitative measurement of brain tissue parameters based on magnetic resonance fingerprinting and its preliminary application in brain diseases
1
2020
... 磁共振指纹(Magnetic Resonance Fingerprinting,MRF)成像由凯斯西储大学的Mark Griswold教授团队于2013年首次提出[1 ,2 ] .该技术通过伪随机脉冲激发受检组织,使不同组织生成独特的时变暂态弛豫响应信号,即MRF信号.在频域完成数据采集后,通过逆傅里叶变换重建获得时域信号.同时,基于磁共振信号激发的布洛赫方程,构建一个包含各种人体组织理论MRF信号的字典.通过模式匹配算法,将重建信号与字典中的理论信号进行比对,从而获得多个定量参数,例如自旋-晶格弛豫时间(Spin-lattice Relaxation Time,T 1 )和自旋-自旋弛豫时间(Spin-spin Relaxation Time,T 2 ).这些定量参数能够客观反映组织的生理状态及病理变化,为疾病的早期诊断和疗效评估提供了重要依据.前瞻性临床应用研究表明,MRF成像技术在心脑血管、肿瘤及神经系统等疾病[3 -4 ] 的早期诊断和病理分级方面中展现出显著优势. 然而,为提升信号特异性并加速数据采集,MRF成像通常采用高倍欠采样策略,仅采集少量数据(约2%~8%)[5 ] 用于定量成像. 这导致逆傅里叶变换重建的时域MRF图像中出现严重的混叠伪影,进而降低定量成像的精度. ...
基于磁共振指纹技术的脑组织参数定量检测及在脑疾病中的初步应用
1
2020
... 磁共振指纹(Magnetic Resonance Fingerprinting,MRF)成像由凯斯西储大学的Mark Griswold教授团队于2013年首次提出[1 ,2 ] .该技术通过伪随机脉冲激发受检组织,使不同组织生成独特的时变暂态弛豫响应信号,即MRF信号.在频域完成数据采集后,通过逆傅里叶变换重建获得时域信号.同时,基于磁共振信号激发的布洛赫方程,构建一个包含各种人体组织理论MRF信号的字典.通过模式匹配算法,将重建信号与字典中的理论信号进行比对,从而获得多个定量参数,例如自旋-晶格弛豫时间(Spin-lattice Relaxation Time,T 1 )和自旋-自旋弛豫时间(Spin-spin Relaxation Time,T 2 ).这些定量参数能够客观反映组织的生理状态及病理变化,为疾病的早期诊断和疗效评估提供了重要依据.前瞻性临床应用研究表明,MRF成像技术在心脑血管、肿瘤及神经系统等疾病[3 -4 ] 的早期诊断和病理分级方面中展现出显著优势. 然而,为提升信号特异性并加速数据采集,MRF成像通常采用高倍欠采样策略,仅采集少量数据(约2%~8%)[5 ] 用于定量成像. 这导致逆傅里叶变换重建的时域MRF图像中出现严重的混叠伪影,进而降低定量成像的精度. ...
Magnetic resonance fingerprinting: an overview
2
2021
... 磁共振指纹(Magnetic Resonance Fingerprinting,MRF)成像由凯斯西储大学的Mark Griswold教授团队于2013年首次提出[1 ,2 ] .该技术通过伪随机脉冲激发受检组织,使不同组织生成独特的时变暂态弛豫响应信号,即MRF信号.在频域完成数据采集后,通过逆傅里叶变换重建获得时域信号.同时,基于磁共振信号激发的布洛赫方程,构建一个包含各种人体组织理论MRF信号的字典.通过模式匹配算法,将重建信号与字典中的理论信号进行比对,从而获得多个定量参数,例如自旋-晶格弛豫时间(Spin-lattice Relaxation Time,T 1 )和自旋-自旋弛豫时间(Spin-spin Relaxation Time,T 2 ).这些定量参数能够客观反映组织的生理状态及病理变化,为疾病的早期诊断和疗效评估提供了重要依据.前瞻性临床应用研究表明,MRF成像技术在心脑血管、肿瘤及神经系统等疾病[3 -4 ] 的早期诊断和病理分级方面中展现出显著优势. 然而,为提升信号特异性并加速数据采集,MRF成像通常采用高倍欠采样策略,仅采集少量数据(约2%~8%)[5 ] 用于定量成像. 这导致逆傅里叶变换重建的时域MRF图像中出现严重的混叠伪影,进而降低定量成像的精度. ...
... MRF成像中的数据采集[5 ] 可以表示为如下线性模型: ...
A compressed sensing framework for magnetic resonance fingerprinting
6
2014
... 近年来,研究者们已相继提出多种重建方法,旨在克服欠采样伪影的影响,进而提升定量成像精度.Davis等[6 ] 提出了一种在压缩感知理论框架下应用的布洛赫响应流形投影方法(Bloch Response Recovery via Iterative Projection,BLIP),有效利用指纹字典内的先验信息,优化数据重建质量.Zhao等[7 ] 则提出了基于最大似然估计的重建方法(MBIR),旨在直接从高度欠采样的测量数据中精确估计定量参数图.然而,上述方法在很大程度上忽略了MRF数据在时间和空间维度上的相关性,限制了定量成像精度的进一步提升.为此,最新的研究工作聚焦于充分挖掘MRF数据的时-空相关冗余,以期进一步提升重建质量.Mazor等[8 ] 提出了一种基于低秩与子空间投影的重建方法(FLOR),将MRF数据按时间帧列化为二维低秩矩阵,有效提升了重建的质量与速度.此后,Zhao等[9 ] 进一步引入低秩张量模型,显著缓解了低秩重建方法中矩阵预处理步骤可能导致的信息损失问题.Cruz等[10 ] 则开发了一种融合稀疏性和局部低秩正则化的重建方法,实现了更短的扫描时间和更高的空间分辨率.Hu等[11 ] 提出了结构化低秩矩阵补全与子空间投影框架(Structured Low-rank Matrix Completion and Subspace Projection,SL-SP),旨在从高度欠采样的测量数据中恢复高质量的MRF数据,从而提升定量成像精度.总体而言,现有方法主要依赖于数据先验模型,并充分利用MRF数据的低秩性、稀疏性及平滑性[12 ] 等固有特性,进而在压缩感知理论框架下进行模型优化,以有效抑制欠采样伪影并重建高质量时域图像.然而,值得关注的是,基于数据先验的约束模型难以充分表征布洛赫成像模型中复杂的时间维度特征,且在定量精度与计算效率之间依然存在难以调和的矛盾,难以兼顾临床应用对实时性和高精度的双重需求. ...
... 根据MRF成像机理[6 ] ,MRF数据$\mathsf{\mathcal{X}}$
... 其中,${{\rho }_{i,j}}\in {{\mathbb{R}}_{+}}$ ${{\eta }_{i,j}}=[{{T}_{1}},{{T}_{2}},\cdots ]$ $\theta $ $\mathbf{B}(\cdot ):{{\mathbb{R}}^{2}}\to {{\mathbb{C}}^{L}}$ $\mathsf{\mathcal{B}}$ [6 ] .本文中主要考虑三个关键组织参数:纵向弛豫时间 (T 1 )、横向弛豫时间(T 2 )和质子密度(PD),并将有所有可能的组织参数组合构成的数据空间建模为三维参数流形$\mathsf{\mathcal{M}}\in {{\mathbb{R}}^{3}}$ . ...
... 其中,$\{{{\eta }_{m}},\ m=1,\cdots,M\}$ $\mathsf{\mathcal{M}}$ $\mathbf{D}$ $\mathbf{D}$ $\mathsf{\mathcal{B}}$ [6 ] 的离散化近似.多参数定量图像可以通过将重建的MRF数据$\mathsf{\hat{\mathcal{X}}}$ [1 ] ,这一过程可以表示为:$\hat{M}={{\Phi }_{\mathbf{D}}}(\mathsf{\hat{\mathcal{X}}})$ $\hat{M}$ ${{\Phi }_{\mathbf{D}}}(\cdot )$ [1 ,11 ] 可以通过预计算的字典$\mathbf{D}$
... 布洛赫流形$\mathsf{\mathcal{B}}$ L 维欧式空间中的一个2-流形,其中L 表示指纹信号的帧长度.此外,本文用$\mathsf{\mathcal{S}}$ $\mathsf{\mathcal{S}}$ $\mathsf{\mathcal{B}}$ [6 ,31 ] ,是嵌入在L 维空间中的一个3-流形.表1 中列出了本文使用的流形相关的重要符号及其定义. ...
... 为验证所提出方法的有效性,本文在模拟数据和体内实采数据上分别开展了重建实验,并与几种当前最先进(SOTA)的方法进行了比较,这些方法包括:基于迭代投影的重建方法(BLIP)[6 ] 、基于模型的迭代重建方法(MBIR)[7 ] 、基于低秩的快速重建方法(FLOR)[8 ] 、基于结构低秩与子空间投影的重建方法(SL-SP)[11 ] 以及基于低秩约束与深度生成先验的重建方法(DG-LR)[36 ] .此外,为了进一步验证所提出方法的有效性,实验中还纳入了仅使用流形结构正则化项(MS)和仅使用局部低秩约束(LLR)的重建结果作为消融实验(Ablation Study).所有涉及方法的实验参数均经过调优,以确保各方法在最佳性能下进行公平对比. ...
Maximum likelihood reconstruction for magnetic resonance fingerprinting
2
2016
... 近年来,研究者们已相继提出多种重建方法,旨在克服欠采样伪影的影响,进而提升定量成像精度.Davis等[6 ] 提出了一种在压缩感知理论框架下应用的布洛赫响应流形投影方法(Bloch Response Recovery via Iterative Projection,BLIP),有效利用指纹字典内的先验信息,优化数据重建质量.Zhao等[7 ] 则提出了基于最大似然估计的重建方法(MBIR),旨在直接从高度欠采样的测量数据中精确估计定量参数图.然而,上述方法在很大程度上忽略了MRF数据在时间和空间维度上的相关性,限制了定量成像精度的进一步提升.为此,最新的研究工作聚焦于充分挖掘MRF数据的时-空相关冗余,以期进一步提升重建质量.Mazor等[8 ] 提出了一种基于低秩与子空间投影的重建方法(FLOR),将MRF数据按时间帧列化为二维低秩矩阵,有效提升了重建的质量与速度.此后,Zhao等[9 ] 进一步引入低秩张量模型,显著缓解了低秩重建方法中矩阵预处理步骤可能导致的信息损失问题.Cruz等[10 ] 则开发了一种融合稀疏性和局部低秩正则化的重建方法,实现了更短的扫描时间和更高的空间分辨率.Hu等[11 ] 提出了结构化低秩矩阵补全与子空间投影框架(Structured Low-rank Matrix Completion and Subspace Projection,SL-SP),旨在从高度欠采样的测量数据中恢复高质量的MRF数据,从而提升定量成像精度.总体而言,现有方法主要依赖于数据先验模型,并充分利用MRF数据的低秩性、稀疏性及平滑性[12 ] 等固有特性,进而在压缩感知理论框架下进行模型优化,以有效抑制欠采样伪影并重建高质量时域图像.然而,值得关注的是,基于数据先验的约束模型难以充分表征布洛赫成像模型中复杂的时间维度特征,且在定量精度与计算效率之间依然存在难以调和的矛盾,难以兼顾临床应用对实时性和高精度的双重需求. ...
... 为验证所提出方法的有效性,本文在模拟数据和体内实采数据上分别开展了重建实验,并与几种当前最先进(SOTA)的方法进行了比较,这些方法包括:基于迭代投影的重建方法(BLIP)[6 ] 、基于模型的迭代重建方法(MBIR)[7 ] 、基于低秩的快速重建方法(FLOR)[8 ] 、基于结构低秩与子空间投影的重建方法(SL-SP)[11 ] 以及基于低秩约束与深度生成先验的重建方法(DG-LR)[36 ] .此外,为了进一步验证所提出方法的有效性,实验中还纳入了仅使用流形结构正则化项(MS)和仅使用局部低秩约束(LLR)的重建结果作为消融实验(Ablation Study).所有涉及方法的实验参数均经过调优,以确保各方法在最佳性能下进行公平对比. ...
Low-rank magnetic resonance fingerprinting
3
2018
... 近年来,研究者们已相继提出多种重建方法,旨在克服欠采样伪影的影响,进而提升定量成像精度.Davis等[6 ] 提出了一种在压缩感知理论框架下应用的布洛赫响应流形投影方法(Bloch Response Recovery via Iterative Projection,BLIP),有效利用指纹字典内的先验信息,优化数据重建质量.Zhao等[7 ] 则提出了基于最大似然估计的重建方法(MBIR),旨在直接从高度欠采样的测量数据中精确估计定量参数图.然而,上述方法在很大程度上忽略了MRF数据在时间和空间维度上的相关性,限制了定量成像精度的进一步提升.为此,最新的研究工作聚焦于充分挖掘MRF数据的时-空相关冗余,以期进一步提升重建质量.Mazor等[8 ] 提出了一种基于低秩与子空间投影的重建方法(FLOR),将MRF数据按时间帧列化为二维低秩矩阵,有效提升了重建的质量与速度.此后,Zhao等[9 ] 进一步引入低秩张量模型,显著缓解了低秩重建方法中矩阵预处理步骤可能导致的信息损失问题.Cruz等[10 ] 则开发了一种融合稀疏性和局部低秩正则化的重建方法,实现了更短的扫描时间和更高的空间分辨率.Hu等[11 ] 提出了结构化低秩矩阵补全与子空间投影框架(Structured Low-rank Matrix Completion and Subspace Projection,SL-SP),旨在从高度欠采样的测量数据中恢复高质量的MRF数据,从而提升定量成像精度.总体而言,现有方法主要依赖于数据先验模型,并充分利用MRF数据的低秩性、稀疏性及平滑性[12 ] 等固有特性,进而在压缩感知理论框架下进行模型优化,以有效抑制欠采样伪影并重建高质量时域图像.然而,值得关注的是,基于数据先验的约束模型难以充分表征布洛赫成像模型中复杂的时间维度特征,且在定量精度与计算效率之间依然存在难以调和的矛盾,难以兼顾临床应用对实时性和高精度的双重需求. ...
... 为验证所提出方法的有效性,本文在模拟数据和体内实采数据上分别开展了重建实验,并与几种当前最先进(SOTA)的方法进行了比较,这些方法包括:基于迭代投影的重建方法(BLIP)[6 ] 、基于模型的迭代重建方法(MBIR)[7 ] 、基于低秩的快速重建方法(FLOR)[8 ] 、基于结构低秩与子空间投影的重建方法(SL-SP)[11 ] 以及基于低秩约束与深度生成先验的重建方法(DG-LR)[36 ] .此外,为了进一步验证所提出方法的有效性,实验中还纳入了仅使用流形结构正则化项(MS)和仅使用局部低秩约束(LLR)的重建结果作为消融实验(Ablation Study).所有涉及方法的实验参数均经过调优,以确保各方法在最佳性能下进行公平对比. ...
... 仿真实验参考了先前主流研究[8 ,11 ] 的实验设置,利用已知的定量参数图对每种算法的重建性能进行了评估.组织定量参数图的真值由三个已知的定量参数矩阵组成,其参数范围分别为T 1 $\in $ T 2 $\in $ $\in $ k 空间系数,中心区域尺寸为20 cm,视场(FOV)为24 cm[详见图3(e) ],对应的采样率约为5%.为了模拟含噪欠采样的测量数据,在k 空间数据中添加了标准差为0.5的复高斯白噪声,对应的信噪比为29 dB. ...
Improved magnetic resonance fingerprinting reconstruction with low-rank and sssubspace modeling
1
2018
... 近年来,研究者们已相继提出多种重建方法,旨在克服欠采样伪影的影响,进而提升定量成像精度.Davis等[6 ] 提出了一种在压缩感知理论框架下应用的布洛赫响应流形投影方法(Bloch Response Recovery via Iterative Projection,BLIP),有效利用指纹字典内的先验信息,优化数据重建质量.Zhao等[7 ] 则提出了基于最大似然估计的重建方法(MBIR),旨在直接从高度欠采样的测量数据中精确估计定量参数图.然而,上述方法在很大程度上忽略了MRF数据在时间和空间维度上的相关性,限制了定量成像精度的进一步提升.为此,最新的研究工作聚焦于充分挖掘MRF数据的时-空相关冗余,以期进一步提升重建质量.Mazor等[8 ] 提出了一种基于低秩与子空间投影的重建方法(FLOR),将MRF数据按时间帧列化为二维低秩矩阵,有效提升了重建的质量与速度.此后,Zhao等[9 ] 进一步引入低秩张量模型,显著缓解了低秩重建方法中矩阵预处理步骤可能导致的信息损失问题.Cruz等[10 ] 则开发了一种融合稀疏性和局部低秩正则化的重建方法,实现了更短的扫描时间和更高的空间分辨率.Hu等[11 ] 提出了结构化低秩矩阵补全与子空间投影框架(Structured Low-rank Matrix Completion and Subspace Projection,SL-SP),旨在从高度欠采样的测量数据中恢复高质量的MRF数据,从而提升定量成像精度.总体而言,现有方法主要依赖于数据先验模型,并充分利用MRF数据的低秩性、稀疏性及平滑性[12 ] 等固有特性,进而在压缩感知理论框架下进行模型优化,以有效抑制欠采样伪影并重建高质量时域图像.然而,值得关注的是,基于数据先验的约束模型难以充分表征布洛赫成像模型中复杂的时间维度特征,且在定量精度与计算效率之间依然存在难以调和的矛盾,难以兼顾临床应用对实时性和高精度的双重需求. ...
Sparsity and locally low rank regularization for MR fingerprinting
1
2019
... 近年来,研究者们已相继提出多种重建方法,旨在克服欠采样伪影的影响,进而提升定量成像精度.Davis等[6 ] 提出了一种在压缩感知理论框架下应用的布洛赫响应流形投影方法(Bloch Response Recovery via Iterative Projection,BLIP),有效利用指纹字典内的先验信息,优化数据重建质量.Zhao等[7 ] 则提出了基于最大似然估计的重建方法(MBIR),旨在直接从高度欠采样的测量数据中精确估计定量参数图.然而,上述方法在很大程度上忽略了MRF数据在时间和空间维度上的相关性,限制了定量成像精度的进一步提升.为此,最新的研究工作聚焦于充分挖掘MRF数据的时-空相关冗余,以期进一步提升重建质量.Mazor等[8 ] 提出了一种基于低秩与子空间投影的重建方法(FLOR),将MRF数据按时间帧列化为二维低秩矩阵,有效提升了重建的质量与速度.此后,Zhao等[9 ] 进一步引入低秩张量模型,显著缓解了低秩重建方法中矩阵预处理步骤可能导致的信息损失问题.Cruz等[10 ] 则开发了一种融合稀疏性和局部低秩正则化的重建方法,实现了更短的扫描时间和更高的空间分辨率.Hu等[11 ] 提出了结构化低秩矩阵补全与子空间投影框架(Structured Low-rank Matrix Completion and Subspace Projection,SL-SP),旨在从高度欠采样的测量数据中恢复高质量的MRF数据,从而提升定量成像精度.总体而言,现有方法主要依赖于数据先验模型,并充分利用MRF数据的低秩性、稀疏性及平滑性[12 ] 等固有特性,进而在压缩感知理论框架下进行模型优化,以有效抑制欠采样伪影并重建高质量时域图像.然而,值得关注的是,基于数据先验的约束模型难以充分表征布洛赫成像模型中复杂的时间维度特征,且在定量精度与计算效率之间依然存在难以调和的矛盾,难以兼顾临床应用对实时性和高精度的双重需求. ...
High-quality MR fingerprinting reconstruction using structured low-rank matrix completion and subspace projection
6
2021
... 近年来,研究者们已相继提出多种重建方法,旨在克服欠采样伪影的影响,进而提升定量成像精度.Davis等[6 ] 提出了一种在压缩感知理论框架下应用的布洛赫响应流形投影方法(Bloch Response Recovery via Iterative Projection,BLIP),有效利用指纹字典内的先验信息,优化数据重建质量.Zhao等[7 ] 则提出了基于最大似然估计的重建方法(MBIR),旨在直接从高度欠采样的测量数据中精确估计定量参数图.然而,上述方法在很大程度上忽略了MRF数据在时间和空间维度上的相关性,限制了定量成像精度的进一步提升.为此,最新的研究工作聚焦于充分挖掘MRF数据的时-空相关冗余,以期进一步提升重建质量.Mazor等[8 ] 提出了一种基于低秩与子空间投影的重建方法(FLOR),将MRF数据按时间帧列化为二维低秩矩阵,有效提升了重建的质量与速度.此后,Zhao等[9 ] 进一步引入低秩张量模型,显著缓解了低秩重建方法中矩阵预处理步骤可能导致的信息损失问题.Cruz等[10 ] 则开发了一种融合稀疏性和局部低秩正则化的重建方法,实现了更短的扫描时间和更高的空间分辨率.Hu等[11 ] 提出了结构化低秩矩阵补全与子空间投影框架(Structured Low-rank Matrix Completion and Subspace Projection,SL-SP),旨在从高度欠采样的测量数据中恢复高质量的MRF数据,从而提升定量成像精度.总体而言,现有方法主要依赖于数据先验模型,并充分利用MRF数据的低秩性、稀疏性及平滑性[12 ] 等固有特性,进而在压缩感知理论框架下进行模型优化,以有效抑制欠采样伪影并重建高质量时域图像.然而,值得关注的是,基于数据先验的约束模型难以充分表征布洛赫成像模型中复杂的时间维度特征,且在定量精度与计算效率之间依然存在难以调和的矛盾,难以兼顾临床应用对实时性和高精度的双重需求. ...
... 其中,$\{{{\eta }_{m}},\ m=1,\cdots,M\}$ $\mathsf{\mathcal{M}}$ $\mathbf{D}$ $\mathbf{D}$ $\mathsf{\mathcal{B}}$ [6 ] 的离散化近似.多参数定量图像可以通过将重建的MRF数据$\mathsf{\hat{\mathcal{X}}}$ [1 ] ,这一过程可以表示为:$\hat{M}={{\Phi }_{\mathbf{D}}}(\mathsf{\hat{\mathcal{X}}})$ $\hat{M}$ ${{\Phi }_{\mathbf{D}}}(\cdot )$ [1 ,11 ] 可以通过预计算的字典$\mathbf{D}$
... 其中,$\mathbf{d}$ $\mathsf{\mathcal{S}}$ $\mathbf{D}$ [11 ] . ...
... 为验证所提出方法的有效性,本文在模拟数据和体内实采数据上分别开展了重建实验,并与几种当前最先进(SOTA)的方法进行了比较,这些方法包括:基于迭代投影的重建方法(BLIP)[6 ] 、基于模型的迭代重建方法(MBIR)[7 ] 、基于低秩的快速重建方法(FLOR)[8 ] 、基于结构低秩与子空间投影的重建方法(SL-SP)[11 ] 以及基于低秩约束与深度生成先验的重建方法(DG-LR)[36 ] .此外,为了进一步验证所提出方法的有效性,实验中还纳入了仅使用流形结构正则化项(MS)和仅使用局部低秩约束(LLR)的重建结果作为消融实验(Ablation Study).所有涉及方法的实验参数均经过调优,以确保各方法在最佳性能下进行公平对比. ...
... 仿真实验参考了先前主流研究[8 ,11 ] 的实验设置,利用已知的定量参数图对每种算法的重建性能进行了评估.组织定量参数图的真值由三个已知的定量参数矩阵组成,其参数范围分别为T 1 $\in $ T 2 $\in $ $\in $ k 空间系数,中心区域尺寸为20 cm,视场(FOV)为24 cm[详见图3(e) ],对应的采样率约为5%.为了模拟含噪欠采样的测量数据,在k 空间数据中添加了标准差为0.5的复高斯白噪声,对应的信噪比为29 dB. ...
... 本节使用在一台3T西门子Prisma磁共振扫描仪上采集的健康人脑实采数据进行实验.实验采用16通道头线圈以及螺旋采样轨迹[见图3(c) ],每帧采集2 880个采样点,对应的采样率约为6%,其他主要成像参数包括视场(FOV)220×220 mm2 ,层厚5 mm.由于实采数据无法获取全采样的真值,实验中遵循先前研究[11 ] 的策略,将原始MRF成像方法在采集长度为1 000时估计的定量参数图作为参考值. ...
Multicomponent MR fingerprinting reconstruction using joint-sparsity and low-rank constraints
1
2023
... 近年来,研究者们已相继提出多种重建方法,旨在克服欠采样伪影的影响,进而提升定量成像精度.Davis等[6 ] 提出了一种在压缩感知理论框架下应用的布洛赫响应流形投影方法(Bloch Response Recovery via Iterative Projection,BLIP),有效利用指纹字典内的先验信息,优化数据重建质量.Zhao等[7 ] 则提出了基于最大似然估计的重建方法(MBIR),旨在直接从高度欠采样的测量数据中精确估计定量参数图.然而,上述方法在很大程度上忽略了MRF数据在时间和空间维度上的相关性,限制了定量成像精度的进一步提升.为此,最新的研究工作聚焦于充分挖掘MRF数据的时-空相关冗余,以期进一步提升重建质量.Mazor等[8 ] 提出了一种基于低秩与子空间投影的重建方法(FLOR),将MRF数据按时间帧列化为二维低秩矩阵,有效提升了重建的质量与速度.此后,Zhao等[9 ] 进一步引入低秩张量模型,显著缓解了低秩重建方法中矩阵预处理步骤可能导致的信息损失问题.Cruz等[10 ] 则开发了一种融合稀疏性和局部低秩正则化的重建方法,实现了更短的扫描时间和更高的空间分辨率.Hu等[11 ] 提出了结构化低秩矩阵补全与子空间投影框架(Structured Low-rank Matrix Completion and Subspace Projection,SL-SP),旨在从高度欠采样的测量数据中恢复高质量的MRF数据,从而提升定量成像精度.总体而言,现有方法主要依赖于数据先验模型,并充分利用MRF数据的低秩性、稀疏性及平滑性[12 ] 等固有特性,进而在压缩感知理论框架下进行模型优化,以有效抑制欠采样伪影并重建高质量时域图像.然而,值得关注的是,基于数据先验的约束模型难以充分表征布洛赫成像模型中复杂的时间维度特征,且在定量精度与计算效率之间依然存在难以调和的矛盾,难以兼顾临床应用对实时性和高精度的双重需求. ...
SVD compression for magnetic resonance fingerprinting in the time domain
1
2014
... 除上述致力于提升MRF数据重建质量的研究方向外,另一些研究工作则着眼于改进模式匹配方法,以期实现高精度的参数量化.McGivney等[13 ] 提出利用奇异值分解将字典和体素指纹投影到时间域上的低维子空间,并在低维子空间中进行模式匹配,从而有效减少了匹配时间和计算开销.Yang等[14 ] 进一步提出使用随机奇异值分解直接估计低维字典子空间,进一步降低了模式匹配的计算时间,并有效减少了指纹字典的内存需求.然而,必须指出的是,基于字典压缩的方法不可避免地会造成部分信息的丢失,进而在一定程度上牺牲了参数估计的精度.为了有效解决这一问题,基于深度学习的方法逐渐成为MRF成像中模式匹配方法的主流方案.Cohen等[15 ] 提出了一种四层全连接神经网络,用于构建信号到参数的映射,有效取代了占用大量内存的字典和计算耗时的字典匹配过程.Oksuz等[16 ] 提出了一种循环神经网络,充分利用组织指纹的时间维度相关信息,有效提高定量成像的精度.Fang等[17 ] 设计了一种两段式深度学习模型(SCQ),整合了全连接网络与U-Net,在四倍加速采集条件下实现了精准的参数重建.Soyak等[18 ] 则提出了一种包含通道注意力模块和全卷积网络的神经网络,并进一步采用重叠块策略进行块级多参数估计,从而有效地减少了参数重建误差.然而,深度学习技术在MRF领域的应用依然受到大规模训练数据集需求的限制,且模型训练与优化依然面临挑战.此外,现有研究大多采用传统图像处理领域业已成熟的网络结构,其在MRF成像领域的泛化能力仍有待进一步验证. ...
Low rank approximation methods for MR fingerprinting with large scale dictionaries
1
2018
... 除上述致力于提升MRF数据重建质量的研究方向外,另一些研究工作则着眼于改进模式匹配方法,以期实现高精度的参数量化.McGivney等[13 ] 提出利用奇异值分解将字典和体素指纹投影到时间域上的低维子空间,并在低维子空间中进行模式匹配,从而有效减少了匹配时间和计算开销.Yang等[14 ] 进一步提出使用随机奇异值分解直接估计低维字典子空间,进一步降低了模式匹配的计算时间,并有效减少了指纹字典的内存需求.然而,必须指出的是,基于字典压缩的方法不可避免地会造成部分信息的丢失,进而在一定程度上牺牲了参数估计的精度.为了有效解决这一问题,基于深度学习的方法逐渐成为MRF成像中模式匹配方法的主流方案.Cohen等[15 ] 提出了一种四层全连接神经网络,用于构建信号到参数的映射,有效取代了占用大量内存的字典和计算耗时的字典匹配过程.Oksuz等[16 ] 提出了一种循环神经网络,充分利用组织指纹的时间维度相关信息,有效提高定量成像的精度.Fang等[17 ] 设计了一种两段式深度学习模型(SCQ),整合了全连接网络与U-Net,在四倍加速采集条件下实现了精准的参数重建.Soyak等[18 ] 则提出了一种包含通道注意力模块和全卷积网络的神经网络,并进一步采用重叠块策略进行块级多参数估计,从而有效地减少了参数重建误差.然而,深度学习技术在MRF领域的应用依然受到大规模训练数据集需求的限制,且模型训练与优化依然面临挑战.此外,现有研究大多采用传统图像处理领域业已成熟的网络结构,其在MRF成像领域的泛化能力仍有待进一步验证. ...
MR fingerprinting deep reconstruction network (DRONE)
1
2018
... 除上述致力于提升MRF数据重建质量的研究方向外,另一些研究工作则着眼于改进模式匹配方法,以期实现高精度的参数量化.McGivney等[13 ] 提出利用奇异值分解将字典和体素指纹投影到时间域上的低维子空间,并在低维子空间中进行模式匹配,从而有效减少了匹配时间和计算开销.Yang等[14 ] 进一步提出使用随机奇异值分解直接估计低维字典子空间,进一步降低了模式匹配的计算时间,并有效减少了指纹字典的内存需求.然而,必须指出的是,基于字典压缩的方法不可避免地会造成部分信息的丢失,进而在一定程度上牺牲了参数估计的精度.为了有效解决这一问题,基于深度学习的方法逐渐成为MRF成像中模式匹配方法的主流方案.Cohen等[15 ] 提出了一种四层全连接神经网络,用于构建信号到参数的映射,有效取代了占用大量内存的字典和计算耗时的字典匹配过程.Oksuz等[16 ] 提出了一种循环神经网络,充分利用组织指纹的时间维度相关信息,有效提高定量成像的精度.Fang等[17 ] 设计了一种两段式深度学习模型(SCQ),整合了全连接网络与U-Net,在四倍加速采集条件下实现了精准的参数重建.Soyak等[18 ] 则提出了一种包含通道注意力模块和全卷积网络的神经网络,并进一步采用重叠块策略进行块级多参数估计,从而有效地减少了参数重建误差.然而,深度学习技术在MRF领域的应用依然受到大规模训练数据集需求的限制,且模型训练与优化依然面临挑战.此外,现有研究大多采用传统图像处理领域业已成熟的网络结构,其在MRF成像领域的泛化能力仍有待进一步验证. ...
Magnetic resonance fingerprinting using recurrent neural networks
1
2019
... 除上述致力于提升MRF数据重建质量的研究方向外,另一些研究工作则着眼于改进模式匹配方法,以期实现高精度的参数量化.McGivney等[13 ] 提出利用奇异值分解将字典和体素指纹投影到时间域上的低维子空间,并在低维子空间中进行模式匹配,从而有效减少了匹配时间和计算开销.Yang等[14 ] 进一步提出使用随机奇异值分解直接估计低维字典子空间,进一步降低了模式匹配的计算时间,并有效减少了指纹字典的内存需求.然而,必须指出的是,基于字典压缩的方法不可避免地会造成部分信息的丢失,进而在一定程度上牺牲了参数估计的精度.为了有效解决这一问题,基于深度学习的方法逐渐成为MRF成像中模式匹配方法的主流方案.Cohen等[15 ] 提出了一种四层全连接神经网络,用于构建信号到参数的映射,有效取代了占用大量内存的字典和计算耗时的字典匹配过程.Oksuz等[16 ] 提出了一种循环神经网络,充分利用组织指纹的时间维度相关信息,有效提高定量成像的精度.Fang等[17 ] 设计了一种两段式深度学习模型(SCQ),整合了全连接网络与U-Net,在四倍加速采集条件下实现了精准的参数重建.Soyak等[18 ] 则提出了一种包含通道注意力模块和全卷积网络的神经网络,并进一步采用重叠块策略进行块级多参数估计,从而有效地减少了参数重建误差.然而,深度学习技术在MRF领域的应用依然受到大规模训练数据集需求的限制,且模型训练与优化依然面临挑战.此外,现有研究大多采用传统图像处理领域业已成熟的网络结构,其在MRF成像领域的泛化能力仍有待进一步验证. ...
Deep learning for fast and spatially constrained tissue quantification from highly accelerated data in magnetic resonance fingerprinting
1
2019
... 除上述致力于提升MRF数据重建质量的研究方向外,另一些研究工作则着眼于改进模式匹配方法,以期实现高精度的参数量化.McGivney等[13 ] 提出利用奇异值分解将字典和体素指纹投影到时间域上的低维子空间,并在低维子空间中进行模式匹配,从而有效减少了匹配时间和计算开销.Yang等[14 ] 进一步提出使用随机奇异值分解直接估计低维字典子空间,进一步降低了模式匹配的计算时间,并有效减少了指纹字典的内存需求.然而,必须指出的是,基于字典压缩的方法不可避免地会造成部分信息的丢失,进而在一定程度上牺牲了参数估计的精度.为了有效解决这一问题,基于深度学习的方法逐渐成为MRF成像中模式匹配方法的主流方案.Cohen等[15 ] 提出了一种四层全连接神经网络,用于构建信号到参数的映射,有效取代了占用大量内存的字典和计算耗时的字典匹配过程.Oksuz等[16 ] 提出了一种循环神经网络,充分利用组织指纹的时间维度相关信息,有效提高定量成像的精度.Fang等[17 ] 设计了一种两段式深度学习模型(SCQ),整合了全连接网络与U-Net,在四倍加速采集条件下实现了精准的参数重建.Soyak等[18 ] 则提出了一种包含通道注意力模块和全卷积网络的神经网络,并进一步采用重叠块策略进行块级多参数估计,从而有效地减少了参数重建误差.然而,深度学习技术在MRF领域的应用依然受到大规模训练数据集需求的限制,且模型训练与优化依然面临挑战.此外,现有研究大多采用传统图像处理领域业已成熟的网络结构,其在MRF成像领域的泛化能力仍有待进一步验证. ...
Channel attention networks for robust MR fingerprint matching
1
2021
... 除上述致力于提升MRF数据重建质量的研究方向外,另一些研究工作则着眼于改进模式匹配方法,以期实现高精度的参数量化.McGivney等[13 ] 提出利用奇异值分解将字典和体素指纹投影到时间域上的低维子空间,并在低维子空间中进行模式匹配,从而有效减少了匹配时间和计算开销.Yang等[14 ] 进一步提出使用随机奇异值分解直接估计低维字典子空间,进一步降低了模式匹配的计算时间,并有效减少了指纹字典的内存需求.然而,必须指出的是,基于字典压缩的方法不可避免地会造成部分信息的丢失,进而在一定程度上牺牲了参数估计的精度.为了有效解决这一问题,基于深度学习的方法逐渐成为MRF成像中模式匹配方法的主流方案.Cohen等[15 ] 提出了一种四层全连接神经网络,用于构建信号到参数的映射,有效取代了占用大量内存的字典和计算耗时的字典匹配过程.Oksuz等[16 ] 提出了一种循环神经网络,充分利用组织指纹的时间维度相关信息,有效提高定量成像的精度.Fang等[17 ] 设计了一种两段式深度学习模型(SCQ),整合了全连接网络与U-Net,在四倍加速采集条件下实现了精准的参数重建.Soyak等[18 ] 则提出了一种包含通道注意力模块和全卷积网络的神经网络,并进一步采用重叠块策略进行块级多参数估计,从而有效地减少了参数重建误差.然而,深度学习技术在MRF领域的应用依然受到大规模训练数据集需求的限制,且模型训练与优化依然面临挑战.此外,现有研究大多采用传统图像处理领域业已成熟的网络结构,其在MRF成像领域的泛化能力仍有待进一步验证. ...
A global geometric framework for nonlinear dimensionality reduction
3
2000
... 近年来,流形理论凭借其卓越的高维数据低维表征能力,在动态磁共振成像领域得到了日益广泛的应用[19 30 ] .基于流形的方法将连续图像帧或离散测量值抽象为嵌入高维空间中的低维流形上的数据点,并有效利用非线性和非局部流形结构正则化来显著提升重建性能.Poddar等[24 ] 提出了一种开创性的动态磁共振成像方法(SToRM),创新性地通过将图像帧建模为高维空间中光滑低维流形上的离散点集,充分利用数据中的非线性和非局部冗余信息来提升重建性能.在后续研究中,SToRM方法被进一步扩展到带限图像流形[23 ] 和无导航先验流形[24 ] 等多种应用场景.Nakarmi等[27 ] 巧妙地利用核主成分分析方法学习特征空间主成分所描述的潜在流形,并进一步通过特征空间中的低秩约束强化这种结构,从而有效加速了动态磁共振成像.基于流形结构的重建方法在有效挖掘高维数据中的非局部和非线性结构信息方面已然展现了巨大的潜力[28 ] .然而,在实际应用中,在噪声和欠采样伪影的双重干扰下,如何从采集到的高维数据观测样本中准确且稳健地估计潜在流形结构仍然极具挑战. ...
... 流形假设指出,现实世界中的高维观测数据本质上是低维流形在高维欧式空间中的非线性嵌入[19 ,21 -22 ] ,流形的维度通常远低于其所在欧式空间的维度,为便于区分,本文中以n -流形特指维度为n 的低维流形. 图1 展示了经典的瑞士卷流形,其表示一个嵌入在三维欧式空间中的2-流形.从几何上看,该流形本质上是将二维平面在三维欧氏空间中卷曲形成的.瑞士卷流形直观地展示了数据内在结构与外在表现之间的复杂关系.在高维空间中,两点之间的欧式距离往往无法准确反映它们的内在相似性[19 ] .以瑞士卷流形上的两个点$\hat{A}$ $\hat{B}$ 图1 中的黄色实线)显著小于其在流形上的实际距离(红色虚线),其实际距离需要通过流形上的测地距离(红色虚线),或将流形映射回低维平面后再以欧氏距离来精确衡量(A 和B 间红色实线).前者要求对流形的潜在拓扑结构进行精确估计,而后者则依赖于适当的数据降维方法,从其高维嵌入中恢复流形的原始结构.然而,在实际应用中,确定潜在流行的维度并准确估计流形结构仍然是十分困难的问题,这一方面,这需要海量的观测数据以及对数据的充分先验信息;另一方面,退化的观测数据所导致的估计偏差亦会产生显著影响.具体而言,噪声会干扰流形结构的识别,而欠采样则可能导致数据分布的稀疏性和不完整性,从而进一步增加流形建模的难度. ...
... [19 ].以瑞士卷流形上的两个点$\hat{A}$ $\hat{B}$ 图1 中的黄色实线)显著小于其在流形上的实际距离(红色虚线),其实际距离需要通过流形上的测地距离(红色虚线),或将流形映射回低维平面后再以欧氏距离来精确衡量(A 和B 间红色实线).前者要求对流形的潜在拓扑结构进行精确估计,而后者则依赖于适当的数据降维方法,从其高维嵌入中恢复流形的原始结构.然而,在实际应用中,确定潜在流行的维度并准确估计流形结构仍然是十分困难的问题,这一方面,这需要海量的观测数据以及对数据的充分先验信息;另一方面,退化的观测数据所导致的估计偏差亦会产生显著影响.具体而言,噪声会干扰流形结构的识别,而欠采样则可能导致数据分布的稀疏性和不完整性,从而进一步增加流形建模的难度. ...
Dimensionality reduction: a comparative
1
2009
... 实验中,基于扩展相图(extended phase graph,EPG)仿真[37 ] 构建指纹字典,参数离散化方案如下:(1)纵向弛豫时间T 1 的取值范围为[100, 5 000] ms,其中在[100, 2 000] ms范围内的增量为20 ms,在 [2 300, 5 000] ms范围内的增量为300 ms;(2)横向弛豫时间T 2 的取值范围为[20, 1 900] ms,其中在[20 ,100] ms范围内的增量为5 ms,在[110,200] ms范围内的增量为10 ms,在[300, 1 900] ms范围内的增量为200 ms.通过剔除T 1 值小于T 2 值的组合,上述设置下指纹字典共涵盖了3 336种组织指纹响应信号. ...
1
2012
... 流形假设指出,现实世界中的高维观测数据本质上是低维流形在高维欧式空间中的非线性嵌入[19 ,21 -22 ] ,流形的维度通常远低于其所在欧式空间的维度,为便于区分,本文中以n -流形特指维度为n 的低维流形. 图1 展示了经典的瑞士卷流形,其表示一个嵌入在三维欧式空间中的2-流形.从几何上看,该流形本质上是将二维平面在三维欧氏空间中卷曲形成的.瑞士卷流形直观地展示了数据内在结构与外在表现之间的复杂关系.在高维空间中,两点之间的欧式距离往往无法准确反映它们的内在相似性[19 ] .以瑞士卷流形上的两个点$\hat{A}$ $\hat{B}$ 图1 中的黄色实线)显著小于其在流形上的实际距离(红色虚线),其实际距离需要通过流形上的测地距离(红色虚线),或将流形映射回低维平面后再以欧氏距离来精确衡量(A 和B 间红色实线).前者要求对流形的潜在拓扑结构进行精确估计,而后者则依赖于适当的数据降维方法,从其高维嵌入中恢复流形的原始结构.然而,在实际应用中,确定潜在流行的维度并准确估计流形结构仍然是十分困难的问题,这一方面,这需要海量的观测数据以及对数据的充分先验信息;另一方面,退化的观测数据所导致的估计偏差亦会产生显著影响.具体而言,噪声会干扰流形结构的识别,而欠采样则可能导致数据分布的稀疏性和不完整性,从而进一步增加流形建模的难度. ...
1
2023
... 流形假设指出,现实世界中的高维观测数据本质上是低维流形在高维欧式空间中的非线性嵌入[19 ,21 -22 ] ,流形的维度通常远低于其所在欧式空间的维度,为便于区分,本文中以n -流形特指维度为n 的低维流形. 图1 展示了经典的瑞士卷流形,其表示一个嵌入在三维欧式空间中的2-流形.从几何上看,该流形本质上是将二维平面在三维欧氏空间中卷曲形成的.瑞士卷流形直观地展示了数据内在结构与外在表现之间的复杂关系.在高维空间中,两点之间的欧式距离往往无法准确反映它们的内在相似性[19 ] .以瑞士卷流形上的两个点$\hat{A}$ $\hat{B}$ 图1 中的黄色实线)显著小于其在流形上的实际距离(红色虚线),其实际距离需要通过流形上的测地距离(红色虚线),或将流形映射回低维平面后再以欧氏距离来精确衡量(A 和B 间红色实线).前者要求对流形的潜在拓扑结构进行精确估计,而后者则依赖于适当的数据降维方法,从其高维嵌入中恢复流形的原始结构.然而,在实际应用中,确定潜在流行的维度并准确估计流形结构仍然是十分困难的问题,这一方面,这需要海量的观测数据以及对数据的充分先验信息;另一方面,退化的观测数据所导致的估计偏差亦会产生显著影响.具体而言,噪声会干扰流形结构的识别,而欠采样则可能导致数据分布的稀疏性和不完整性,从而进一步增加流形建模的难度. ...
M-MRI: A manifold-based framework to highly accelerated dynamic magnetic resonance imaging
1
2017
... 近年来,流形理论凭借其卓越的高维数据低维表征能力,在动态磁共振成像领域得到了日益广泛的应用[19 30 ] .基于流形的方法将连续图像帧或离散测量值抽象为嵌入高维空间中的低维流形上的数据点,并有效利用非线性和非局部流形结构正则化来显著提升重建性能.Poddar等[24 ] 提出了一种开创性的动态磁共振成像方法(SToRM),创新性地通过将图像帧建模为高维空间中光滑低维流形上的离散点集,充分利用数据中的非线性和非局部冗余信息来提升重建性能.在后续研究中,SToRM方法被进一步扩展到带限图像流形[23 ] 和无导航先验流形[24 ] 等多种应用场景.Nakarmi等[27 ] 巧妙地利用核主成分分析方法学习特征空间主成分所描述的潜在流形,并进一步通过特征空间中的低秩约束强化这种结构,从而有效加速了动态磁共振成像.基于流形结构的重建方法在有效挖掘高维数据中的非局部和非线性结构信息方面已然展现了巨大的潜力[28 ] .然而,在实际应用中,在噪声和欠采样伪影的双重干扰下,如何从采集到的高维数据观测样本中准确且稳健地估计潜在流形结构仍然极具挑战. ...
Dynamic MRI using smoothness regularization on manifolds (SToRM)
4
2015
... 近年来,流形理论凭借其卓越的高维数据低维表征能力,在动态磁共振成像领域得到了日益广泛的应用[19 30 ] .基于流形的方法将连续图像帧或离散测量值抽象为嵌入高维空间中的低维流形上的数据点,并有效利用非线性和非局部流形结构正则化来显著提升重建性能.Poddar等[24 ] 提出了一种开创性的动态磁共振成像方法(SToRM),创新性地通过将图像帧建模为高维空间中光滑低维流形上的离散点集,充分利用数据中的非线性和非局部冗余信息来提升重建性能.在后续研究中,SToRM方法被进一步扩展到带限图像流形[23 ] 和无导航先验流形[24 ] 等多种应用场景.Nakarmi等[27 ] 巧妙地利用核主成分分析方法学习特征空间主成分所描述的潜在流形,并进一步通过特征空间中的低秩约束强化这种结构,从而有效加速了动态磁共振成像.基于流形结构的重建方法在有效挖掘高维数据中的非局部和非线性结构信息方面已然展现了巨大的潜力[28 ] .然而,在实际应用中,在噪声和欠采样伪影的双重干扰下,如何从采集到的高维数据观测样本中准确且稳健地估计潜在流形结构仍然极具挑战. ...
... [24 ]等多种应用场景.Nakarmi等[27 ] 巧妙地利用核主成分分析方法学习特征空间主成分所描述的潜在流形,并进一步通过特征空间中的低秩约束强化这种结构,从而有效加速了动态磁共振成像.基于流形结构的重建方法在有效挖掘高维数据中的非局部和非线性结构信息方面已然展现了巨大的潜力[28 ] .然而,在实际应用中,在噪声和欠采样伪影的双重干扰下,如何从采集到的高维数据观测样本中准确且稳健地估计潜在流形结构仍然极具挑战. ...
... 通过引入图拉普拉斯算子$\mathbf{L}$ [24 26 ] ,流形结构正则化项可重写为矩阵运算形式: ...
... 其中,$\text{Tr}(\cdot )$ $\mathbf{Q}(\mathsf{\mathcal{X}})$ $\mathsf{\mathcal{X}}$ ${{\mathbf{Q}}_{\mathbf{q}}}(\mathsf{\mathcal{X}})$ . 图拉普拉斯算子$\mathbf{L}$ [24 ,33 ] 定义为: ...
Manifold recovery using kernel low-rank regularization: Application to dynamic imaging
0
2019
Free-breathing & ungated cardiac MRI using iterative SToRM (i-SToRM)
1
2019
... 通过引入图拉普拉斯算子$\mathbf{L}$ [24 26 ] ,流形结构正则化项可重写为矩阵运算形式: ...
A kernel-based low-rank (KLR) model for low-dimensional manifold recovery in highly accelerated dynamic MRI
1
2017
... 近年来,流形理论凭借其卓越的高维数据低维表征能力,在动态磁共振成像领域得到了日益广泛的应用[19 30 ] .基于流形的方法将连续图像帧或离散测量值抽象为嵌入高维空间中的低维流形上的数据点,并有效利用非线性和非局部流形结构正则化来显著提升重建性能.Poddar等[24 ] 提出了一种开创性的动态磁共振成像方法(SToRM),创新性地通过将图像帧建模为高维空间中光滑低维流形上的离散点集,充分利用数据中的非线性和非局部冗余信息来提升重建性能.在后续研究中,SToRM方法被进一步扩展到带限图像流形[23 ] 和无导航先验流形[24 ] 等多种应用场景.Nakarmi等[27 ] 巧妙地利用核主成分分析方法学习特征空间主成分所描述的潜在流形,并进一步通过特征空间中的低秩约束强化这种结构,从而有效加速了动态磁共振成像.基于流形结构的重建方法在有效挖掘高维数据中的非局部和非线性结构信息方面已然展现了巨大的潜力[28 ] .然而,在实际应用中,在噪声和欠采样伪影的双重干扰下,如何从采集到的高维数据观测样本中准确且稳健地估计潜在流形结构仍然极具挑战. ...
Kernel regression imputation in manifolds via bi-linear modeling: The dynamic-MRI case
1
2022
... 近年来,流形理论凭借其卓越的高维数据低维表征能力,在动态磁共振成像领域得到了日益广泛的应用[19 30 ] .基于流形的方法将连续图像帧或离散测量值抽象为嵌入高维空间中的低维流形上的数据点,并有效利用非线性和非局部流形结构正则化来显著提升重建性能.Poddar等[24 ] 提出了一种开创性的动态磁共振成像方法(SToRM),创新性地通过将图像帧建模为高维空间中光滑低维流形上的离散点集,充分利用数据中的非线性和非局部冗余信息来提升重建性能.在后续研究中,SToRM方法被进一步扩展到带限图像流形[23 ] 和无导航先验流形[24 ] 等多种应用场景.Nakarmi等[27 ] 巧妙地利用核主成分分析方法学习特征空间主成分所描述的潜在流形,并进一步通过特征空间中的低秩约束强化这种结构,从而有效加速了动态磁共振成像.基于流形结构的重建方法在有效挖掘高维数据中的非局部和非线性结构信息方面已然展现了巨大的潜力[28 ] .然而,在实际应用中,在噪声和欠采样伪影的双重干扰下,如何从采集到的高维数据观测样本中准确且稳健地估计潜在流形结构仍然极具挑战. ...
Manifold learning via linear tangent space alignment (LTSA) for accelerated dynamic MRI with sparse sampling
0
2022
A parallel spatial and Bloch manifold regularized iterative reconstruction method for MR Fingerprinting
1
2021
... 近年来,流形理论凭借其卓越的高维数据低维表征能力,在动态磁共振成像领域得到了日益广泛的应用[19 30 ] .基于流形的方法将连续图像帧或离散测量值抽象为嵌入高维空间中的低维流形上的数据点,并有效利用非线性和非局部流形结构正则化来显著提升重建性能.Poddar等[24 ] 提出了一种开创性的动态磁共振成像方法(SToRM),创新性地通过将图像帧建模为高维空间中光滑低维流形上的离散点集,充分利用数据中的非线性和非局部冗余信息来提升重建性能.在后续研究中,SToRM方法被进一步扩展到带限图像流形[23 ] 和无导航先验流形[24 ] 等多种应用场景.Nakarmi等[27 ] 巧妙地利用核主成分分析方法学习特征空间主成分所描述的潜在流形,并进一步通过特征空间中的低秩约束强化这种结构,从而有效加速了动态磁共振成像.基于流形结构的重建方法在有效挖掘高维数据中的非局部和非线性结构信息方面已然展现了巨大的潜力[28 ] .然而,在实际应用中,在噪声和欠采样伪影的双重干扰下,如何从采集到的高维数据观测样本中准确且稳健地估计潜在流形结构仍然极具挑战. ...
Shrinking cell-like decompositions of manifolds. Codimension three
1
1979
... 布洛赫流形$\mathsf{\mathcal{B}}$ L 维欧式空间中的一个2-流形,其中L 表示指纹信号的帧长度.此外,本文用$\mathsf{\mathcal{S}}$ $\mathsf{\mathcal{S}}$ $\mathsf{\mathcal{B}}$ [6 ,31 ] ,是嵌入在L 维空间中的一个3-流形.表1 中列出了本文使用的流形相关的重要符号及其定义. ...
Quantitative magnetic resonance imaging: From fingerprinting to integrated physics-based models
2
2019
... 根据皮卡-林德洛夫(Picard-Lindelöf)定理[32 ] ,对于任意组织参数组合,其对应的理论指纹响应信号是唯一的.也即,若存在两个不同的组织参数组合${{\eta }_{i}}$ ${{\eta }_{j}}$ ${{\eta }_{i}}={{\eta }_{j}}$
... 此外,布洛赫方程在组织参数和指纹响应信号之间建立了稳定的非线性映射[32 ] ,即: ...
Laplacian eigenmaps for dimensionality reduction and data representation
1
2003
... 其中,$\text{Tr}(\cdot )$ $\mathbf{Q}(\mathsf{\mathcal{X}})$ $\mathsf{\mathcal{X}}$ ${{\mathbf{Q}}_{\mathbf{q}}}(\mathsf{\mathcal{X}})$ . 图拉普拉斯算子$\mathbf{L}$ [24 ,33 ] 定义为: ...
1
2011
... 问题(13)可采用增量次梯度-邻近点方法[34 ] 来迭代求解,第n 次迭代涉及求解以下两个子问题: ...
TorchKbNufft: A high-level, hardware-agnostic non-uniform fast Fourier transform
2
2020
... 本文所提出的方法在一台配备英特尔至强(Intel Xeon)中央处理器(CPU)和英伟达(Nvidia)Quadro GV100图形处理器(GPU)的Linux工作站上进行实现与实验验证.为了更精细地平衡正则化项,流形正则化项的惩罚参数${{\lambda }_{1}}$ $\mathbf{L}$ $\lambda _{1}^{n}=\lambda _{1}^{0}\times \text{max}({{\mathbf{L}}^{n}})$ $\lambda _{1}^{0}$ $\mu =1$ ${{\lambda }_{2}}=0.1$ $\beta =1/5$ . 算法最大迭代次数设置为50.算法中还引入一个由GPU加速的非均匀快速傅里叶变换(NUFFT)库[35 ] ,以在非笛卡尔采样场景中提升所提方法的重建效率. ...
... 所提出的方法通过共享的块提取算子,同时利用了流形结构先验和局部低秩先验.这一设计不仅强化了对数据结构先验信息的利用,还显著降低了算法的计算复杂度.此外,为了进一步提升非笛卡尔采样场景下的计算效率,本文采用了基于GPU加速的非均匀快速傅里叶变换库[35 ] .表7 展示了不同方法在非笛卡尔采样模式下的平均计算时间,实验中采用了变密度螺旋轨迹[图3(e) ],数据采集长度为500.结果表明,与现有的最先进方法(SOTA)相比,所提出方法显著减少了重建耗时.在相同实验场景下,所提出方法的重建耗时仅为其他方法的8.8%~25.0%,充分体现了其在计算效率上的优越性. ...
Accelerated magnetic resonance fingerprinting with low-rank and generative subspace modeling
2
2023
... 为验证所提出方法的有效性,本文在模拟数据和体内实采数据上分别开展了重建实验,并与几种当前最先进(SOTA)的方法进行了比较,这些方法包括:基于迭代投影的重建方法(BLIP)[6 ] 、基于模型的迭代重建方法(MBIR)[7 ] 、基于低秩的快速重建方法(FLOR)[8 ] 、基于结构低秩与子空间投影的重建方法(SL-SP)[11 ] 以及基于低秩约束与深度生成先验的重建方法(DG-LR)[36 ] .此外,为了进一步验证所提出方法的有效性,实验中还纳入了仅使用流形结构正则化项(MS)和仅使用局部低秩约束(LLR)的重建结果作为消融实验(Ablation Study).所有涉及方法的实验参数均经过调优,以确保各方法在最佳性能下进行公平对比. ...
... 所有实验均采用稳态进动快速成像(Fast Imaging with Steady State Precession,FISP)[36 ] 脉冲序列进行数据采集,翻转角(FA)和重复时间(TR)模式如图3 中的(a)、(b)子图所示,回波时间(TE)固定为2.94 ms. 实验中采用了三种不同的采样轨迹,如图3 中的(c)、(d)、(e)子图所示,这些采样轨迹包括螺旋采样轨迹(Spiral)、径向采样轨迹(Radial)和变密度螺旋采样轨迹(Variable density spiral,Vds-spiral),全面验证所提方法在多种数据采集条件下的鲁棒性和适用性. ...
MR fingerprinting using fast imaging with steady state precession (FISP) with spiral readout
1
2015
... 实验中,基于扩展相图(extended phase graph,EPG)仿真[37 ] 构建指纹字典,参数离散化方案如下:(1)纵向弛豫时间T 1 的取值范围为[100, 5 000] ms,其中在[100, 2 000] ms范围内的增量为20 ms,在 [2 300, 5 000] ms范围内的增量为300 ms;(2)横向弛豫时间T 2 的取值范围为[20, 1 900] ms,其中在[20 ,100] ms范围内的增量为5 ms,在[110,200] ms范围内的增量为10 ms,在[300, 1 900] ms范围内的增量为200 ms.通过剔除T 1 值小于T 2 值的组合,上述设置下指纹字典共涵盖了3 336种组织指纹响应信号. ...
Magnetic resonance fingerprinting: a technical review
4
2019
... 图7 和图8 分别展示了不同方法在采集长度为500时对两名健康志愿者各使用一组实采数据重建的参数图.从结果可以看出,BLIP和MBIR方法能够恢复更锐利的图像,但引入了较多类似噪声的孤立点偏差.FLOR和SL-SP方法通过提供更精确的参数估计展示了改进的重建效果.相比之下,所提出的MS-LLR算法在重建参数图中提供了最清晰的组织细节,表现出最佳的重建质量.为进一步评估所提出方法的性能,将图7 和图8 中蓝色框(第1行第1列箭头所指)标注区域内测量的几种典型脑组织的T 1 和T 2 定量成像值与文献报告的值[38 ] 进行了定性比较,比较结果见表3 和表4 .这些典型脑组织包括脑灰质(Gray Matter, GM)、脑白质(White Matter, WM)和脑脊液(Cerebrospinal Fluid, CSF).结果显示,所提出的MS-LLR方法提供了最稳定的参数估计,其估计值与参考值及文献[38 ] 中的报告值最为一致,进一步验证了该方法在实际应用中的可靠性和准确性. ...
... [38 ]中的报告值最为一致,进一步验证了该方法在实际应用中的可靠性和准确性. ...
...
T 1 and
T 2 values (ms, mean ± standard deviation) of several brain tissues measured on the corresponding regions (blue boxes) in
Fig.7 Table 3 REF BLIP MBIR FLOR SL-SP DG-LR MS LLR MS-LLR(本文方法) 文献[38 ] T 1 GM 1342.4±53.7 1328.4±242.2 1325.6±140.2 1319.2±95.6 1327.0±84.5 1322±79.3 1305.4±64.2 1331.4±75.7 1337.1±61.1 1286~1393 WM 797.6±35.3 806.7±104.9 807.2±74.4 810.0±61.2 805.6±56.4 805.8±56.8 789.3±45.5 804.7±50.2 801.2±42.1 788~898 CSF 3412.0±157.8 3653.6±295.7 3528.0±244.1 3524.0±192.7 3452.0±180.4 3441.7±184.2 3143.5±174.1 3459.5±183.7 3432.6±168.5 / T 2 GM 78.4±6.0 93.3±19.8 85.2±17.1 82.8±12.4 80.8±11.2 80.6±11.8 76.8±8.9 80.3±13.5 79.5±7.8 78~117 WM 68.4±4.7 76.2±14.5 72.3±12.1 71.7±8.9 71.2±7.5 70.2±7.6 67.1±5.7 70.5±6.4 69.0±5.1 63~80 CSF 816.0±171.3 857.8±313.6 830.0±248.2 798.6±217.7 802.4±202.9 804.4±195.1 790.1±189.3 807.3±193.9 811.6±187.7 /
10.11938/cjmr20253145.T0004 表4 图8 对应区域(蓝色框)内测量的几种脑组织的T1 和T2 值与参考值的对比(ms,均值±标准差) ...
...
T 1 and
T 2 values (ms, mean ± standard deviation) of several brain tissues measured on the corresponding regions (blue boxes) in
Fig.8 Table 4 REF BLIP MBIR FLOR SL-SP DG-LR MS LLR MS-LLR(本文方法) 文献[38 ] T 1 GM 1347.2±68.7 1327.2±249.5 1314.8±162.4 1321.6±121.9 1316.0±102.1 1324.7±105.4 1299.0±89.7 1309.1±97.6 1331.8±77.6 1286~1393 WM 805.6±79.1 850.1±325.1 852.8±195.5 824.0±127.4 813.6±109.1 816.3±102.1 791.1±58.5 809.5±76.8 804.5±52.3 788~898 CSF 3596.0±183.5 3657.6±327.1 3692.0±285.1 3604.0±243.4 3632.0±224.9 3640.4±226.1 3343.2±212.6 3628.3±216.7 3583.3±203.1 / T 2 GM 80.1±4.8 92.9±24.2 86.6±14.7 83.4±12.9 82.6±10.4 82.8±9.2 77.6±7.1 81.8±9.1 80.9±6.2 78~117 WM 64.4±5.8 76.8±18.0 72.6±11.2 69.4±9.0 67.0±8.4 66.3±8.2 62.8±6.5 66.9±8.3 65.7±6.2 63~80 CSF 804.0±109.1 852.4±225.5 831.2±201.2 828.0±172.2 823.2±160.5 819.8±157.2 783.8±142.4 819.7±145.6 814.9±125.6 /
4 分析与讨论 4.1 超参数设置 图9 展示了不同正则项超参数设置组合下算法的重建性能,其中最优参数组合以黑色方框突出显示.实验中分别使用了螺旋采样轨迹[图3(c) ]和径向采样轨迹[图3(d) ],数据采集长度为500.从结果可以看出,所提出方法在不同的采样轨迹下表现出良好的参数鲁棒性,两种轨迹的最优参数设置高度一致,$\lambda _{1}^{0}$ ${{\lambda }_{2}}$ ${{\lambda }_{2}}$