波谱学杂志, 2025, 42(3): 308-320 doi: 10.11938/cjmr20253150

磁共振仪器与技术专栏

一种用于低场磁共振波谱仪的圆极化线圈设计

汤世豪1,2, 杨谨毓1,2, 徐雅洁,#, 王亚2, 彭博文1,2, 高宇昊1,2, 杨晓冬,2,*

1.中国科学技术大学生物医学工程学院(苏州)，生命科学与医学部，江苏 苏州 215163

2.中国科学院苏州生物医学工程技术研究所，江苏 苏州 215163

A Design of Circularly Polarized Coil for Low-field Nuclear Magnetic Resonance Spectrometers

TANG Shihao1,2, YANG Jinyu1,2, XU Yajie,#, WANG Ya2, PENG Bowen1,2, GAO Yuhao1,2, YANG Xiaodong,2,*

1. School of Biomedical Engineering (Suzhou), Division of Life Sciences and Medicine, University of Science and Technology of China, Suzhou 215163, China

2. Suzhou Institute of Biomedical Engineering and Technology, Chinese Academy of Sciences, Suzhou 215163, China

通讯作者: # Tel: 15250434900, E-mail:xuyj@sibet.ac.cn;* Tel: 18900616030, E-mail:xiaodong.yang@sibet.ac.cn.

收稿日期: 2025-03-17   网络出版日期: 2025-04-07

基金资助: 国家自然科学基金面上项目(12375293); 苏州市社发项目(2023ss23)

Corresponding authors: # Tel: 15250434900, E-mail:xuyj@sibet.ac.cn;* Tel: 18900616030, E-mail:xiaodong.yang@sibet.ac.cn.

Received: 2025-03-17   Online: 2025-04-07

摘要

信噪比（SNR）是影响桌面磁共振波谱仪信号质量的一个关键参数，在探头中使用正交圆极化线圈是提升信噪比的有效手段，由于桌面磁共振波谱仪磁体结构紧凑，留给探头空间有限，对圆极化线圈的设计造成挑战．在桌面磁共振波谱仪中未有其它研究者采用过圆极化线圈．基于实验室自研桌面磁共振波谱仪平台，本文设计并制作了一套基于柔性版的收发一体圆极化线圈，该线圈由一组正交的鞍形线圈和亥姆霍兹线圈构成．首先根据探测目标区域的结构参数确定了单匝线圈的支撑结构与尺寸，然后使用Ansys Maxwell磁场仿真软件确定了圆极化线圈的最优匝数，最后使用自研圆极化探头结合外围射频电路对CuSO4溶液进行了测试并以此评估该圆极化线圈的性能．实验结果表明，组合构成的圆极化线圈与单通道鞍形线圈和亥姆霍兹线圈相比，SNR分别提升了28.78%和29.21%，发射功率约节省了37.5%，证明圆极化线圈能够有效提升桌面磁共振波谱仪探头性能．

关键词： 磁共振波谱（MRS）; 正交线圈; 线圈优化; 双通道探头

Abstract

Signal-to-noise ratio (SNR) is a key parameter governing signal quality in benchtop MRS spectrometers, where quadrature circularly polarized coils offer an effective means to enhance SNR. However, the confined space within the compact magnets of desktop systems poses challenges for implementing such coils—a strategy previously unattempted in this domain. Leveraging a self-developed desktop MRS platform, this study designed and fabricated a flexible printed circuit-based transceiver-integrated circularly polarized coil system, comprising orthogonally arranged saddle and Helmholtz coils. The coil geometry was optimized through Ansys Maxwell simulations, and experimental validation using CuSO₄ solution demonstrated SNR improvements of 28.78% and 29.21% over single-channel saddle and Helmholtz coils, respectively, alongside a 37.5% reduction in reflected power. These results confirm the viability of circularly polarized coils for advancing desktop MRS probe performance.

Keywords： magnetic resonance spectroscopy (MRS); quadrature coils; coil optimization; dual-channel probe

PDF (1368KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

汤世豪, 杨谨毓, 徐雅洁, 王亚, 彭博文, 高宇昊, 杨晓冬. 一种用于低场磁共振波谱仪的圆极化线圈设计[J]. 波谱学杂志, 2025, 42(3): 308-320 doi:10.11938/cjmr20253150

TANG Shihao, YANG Jinyu, XU Yajie, WANG Ya, PENG Bowen, GAO Yuhao, YANG Xiaodong. A Design of Circularly Polarized Coil for Low-field Nuclear Magnetic Resonance Spectrometers[J]. Chinese Journal of Magnetic Resonance, 2025, 42(3): 308-320 doi:10.11938/cjmr20253150

引言

核磁共振（Nuclear Magnetic Resonance，NMR）波谱作为一种非破坏性分析技术，凭借其无电离辐射、样品无损检测等特性，已成为解析生化系统多维结构、动态过程及反应机理的重要工具，在食品质量监控、有机合成表征、药物研发及高分子材料研究等领域具有重要的应用前景[1].近年来，基于永磁体技术的桌面型NMR波谱仪在科研与工业领域发展迅速.相较于传统超导核磁系统，虽然受限于磁场强度（通常0.5 ~ 2 T）导致谱图分辨率与信噪比相对较低，但桌面NMR波谱仪突破性优势体现在两方面：一是体积紧凑；二是无液氦磁体，极大缩减了装机和维护成本[2-3].因此，桌面磁共振波谱仪在高校教学实验室、制药过程监控及工业现场检测等场景展现出独特的应用潜力，为传统高场NMR技术（>10 T）提供了重要补充.

探头是磁共振系统的核心部件，在低场磁共振波谱仪中通常使用单通道射频线圈结构设计，如鞍形线圈、亥姆霍兹线圈结构等.然而常规的单通道线圈信噪比有限，寻求更高效的射频线圈对提高桌面磁共振波谱仪系统性能十分关键.圆极化线圈设计是一种常用的提升探头信噪比的方法，该方法通过增加一个空间上与单通道垂直的线圈来实现探头的圆极化接收效果，实现$\sqrt{2}$倍信噪比的提升.国内外关于磁共振圆极化探头的研究多集中在成像领域.2024年重庆大学徐征团队[4]研究了一种用于超低场磁共振成像系统的膝关节正交接收线圈，该系统支撑结构由半径为80 mm、长度为200 mm的正交线圈组成，实现了图像SNR提升约30%的效果；Hoult等人提出了一种在成像实验下进行圆极化线圈正交检测的理论[5]，预测使用圆极化线圈相对于单线圈可以将图像信噪比提升41%，并节省一半的发射功率.实测图像质量提高了40%，发射机功率降低1/2.上述工作围绕成像系统展开，为满足成像所要求的大视野，线圈体积较大，不适用于桌面磁共振系统.在桌面磁共振波谱仪中尚未发现有研究者使用圆极化探头.基于永磁体的桌面磁共振波谱仪具有结构紧凑，探头尺寸小等特征，导致留给射频线圈设计的空间有限，是紧凑型磁共振波谱仪中圆极化线圈设计存在的主要挑战.

本文基于实验室现有的0.53 T Halbach磁体结构研究紧凑型收发一体圆极化射频探头及配套的Hybrid电桥电路.基于鞍形线圈与亥姆霍兹线圈两种构型，利用电磁仿真软件Ansys Maxwell对样品感兴趣区域进行线圈性能指标的分析，优化相应线圈参数模型；设计了配套的Hybrid电桥电路，进行了性能测试；基于线圈结构仿真的优化结果制作实物，并结合调谐匹配电路安装与调试；最后基于磁体平台，与外围的Hybrid电桥，收/发开关，低噪声前置放大器，射频功率放大器形成射频链路测试，验证圆极化探头的性能.

1 圆极化线圈设计

1.1 圆极化线圈原理

根据线圈发射的磁场特性可分成两种类型：线极化、圆极化.理想条件下，相对于线极化线圈，使用圆极化线圈发射射频脉冲可以节省一半的功率，而圆极化线圈接收可以有效提高谱图的信号质量.下面将简要介绍圆极化探头的理论，分析其如何节省功率及提高信号信噪比.

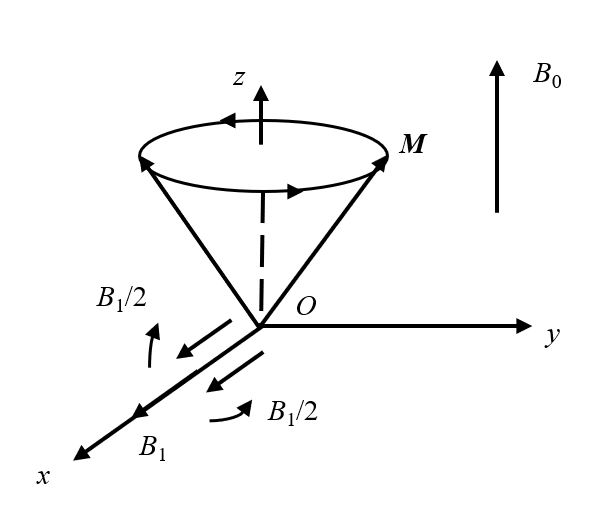
如图1所示，M为磁化矢量.线圈发射的磁场满足：${{B}_{x}}={{B}_{1}}\text{cos}wt$，其中，ω为旋转角频率，t为时间变量，${{B}_{1}}$为脉冲幅值，该线圈为线极化线圈，射频场是沿x方向的余弦振荡脉冲，为了便于分析，将${{B}_{x}}$分解为两个在xOy平面内的旋转矢量之和，即：

${{B}_{x}}=\frac{{{B}_{1}}}{2}(\cos \omega x+jsin\omega x)+\frac{{{B}_{1}}}{2}(\cos \omega x-jsin\omega x)={{B}_{+}}+{{B}_{-}}$

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   线极化发射的射频脉冲

Fig. 1   Linearly polarized RF transmission pulse


每一旋转矢量幅值都为${{B}_{1}}/2$，旋转角频率为ω，但各自旋转方向相反，${{B}_{+}}$逆时针旋转，${{B}_{-}}$顺时针旋转，${{B}_{+}}$的旋转方向与M相同，当${{B}_{+}}$的频率正好等于共振频率时，${{B}_{+}}$分量使M逐渐倒向xOy平面；而${{B}_{-}}$的旋转方向与M相反，${{B}_{-}}$对M的倒向过程不起作用，在磁共振线极化发射系统中，一半分量${{B}_{-}}$实际上被浪费掉，所以线极化发射的效率不高[5].线极化发射线圈以螺线管形、马鞍形、Helmholtz形线圈为代表.

圆极化发射的磁场在xOy平面上满足：

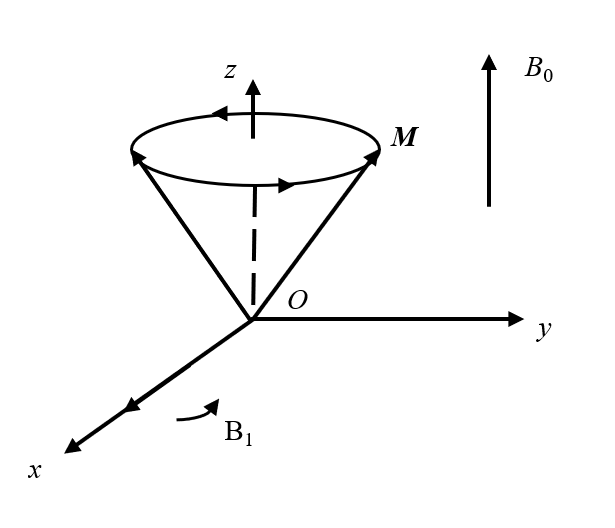
$\left\{\begin{array}{l} B_{x}=B_{1} \cos \omega x \\ B_{y}=B_{1} \sin \omega x \end{array}\right.$

图2为圆极化发射的射频脉冲示意图.磁场随时间的变化轨迹为一个圆，$B_{x}^{2}+B_{y}^{2}=B_{1}^{2}$.如图2所示，图中$B_{x}^{{}}$、$B_{y}^{{}}$的合成矢量$B_{1}^{{}}$与M的旋转方向相同，与线极化发射相比，圆极化发射的效率提高了一倍，如果线极化发射所需功率消耗为P，则圆极化发射所需的功率消耗仅为P/2[5].

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   圆极化发射的射频脉冲

Fig. 2   Circularly polarized RF transmission pulse


接收状态下，根据互易性原理[6]，圆极化探头的两个正交线圈检测到相位差为90˚的自由感应衰减信号.由于噪声在两条通道中是不相关的（随机噪声），而信号是相关的，因此通过电桥调节相位后合并两路自由感应衰减信号，信号幅值增加为原来的2倍，而噪声因不相关叠加仅增加$\sqrt{2}$倍.最终信噪比提升为：

$\text{SN}{{\text{R}}_{\text{cp}}}=\frac{2S}{\sqrt{2}N}=\sqrt{2}\cdot \frac{S}{N}=\sqrt{2}\cdot \text{SN}{{\text{R}}_{\text{lp}}}$

其中，S为线极化线圈接受到的信号幅值，N为线极化线圈接收到的噪声，$\text{SN}{{\text{R}}_{\text{cp}}}$为圆极化线圈信噪比，$\text{SN}{{\text{R}}_{\text{lp}}}$为线极化线圈信噪比.

因此将圆极化线圈应用于桌面磁共振波谱仪有助于解决磁场强度低而导致信噪比差以及发射效率低的问题.

1.2 线圈构型及单匝线圈尺寸选择

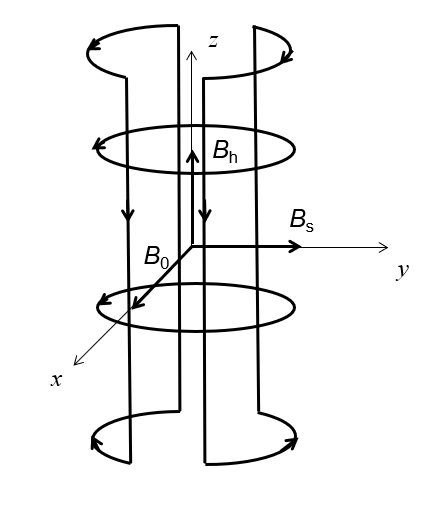
圆极化线圈产生的射频场需相互正交，并且与磁体的主磁场正交.如图3所示，Halbach阵列磁体主磁场B0方向为径向（本设计中为x轴方向）.正交线圈中两组线圈产生的射频场应与主磁场方向垂直，且本身两组线圈产生的射频场也应垂直.鞍形线圈与亥姆霍兹线圈三维构型都为轴向圆柱型，适用于Halbach阵列磁体圆柱形空间，且鞍形线圈能够产生径向射频激发场，亥姆霍兹线圈能够产生轴向射频激发场.因此，本文选择①鞍形线圈，产生与主磁场垂直的射频场Bs（本设计中为y轴方向）；②亥姆霍兹线圈，产生与垂直的射频场Bh（本设计中为z轴方向）.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   Halbach磁体产生的B0场（沿x轴方向），鞍形线圈产生的Bs射频场（沿y轴方向），亥姆霍兹线圈产生的Bh场（沿z轴方向）. 其中线圈上的箭头代表电流方向

Fig. 3   The B0 field generated by the Halbach magnet (along the x-axis direction), the Bs radiofrequency field generated by the saddle coil (along the y-axis direction), and the Bh field generated by the Helmholtz coil (along the z-axis direction). The arrows on the coils indicate the current direction


根据磁共振探头结构和样品管（5 mm标准样品管），首先确定单匝鞍形和亥姆霍兹线圈的尺寸，然后通过仿真软件对线圈匝数进行优化设计，并通过定义的综合性能获取线圈的最佳匝数.最后结合调谐匹配电路进行射频线圈的匹配，使得线圈能够正确工作在实验室低场磁体对应频率上.

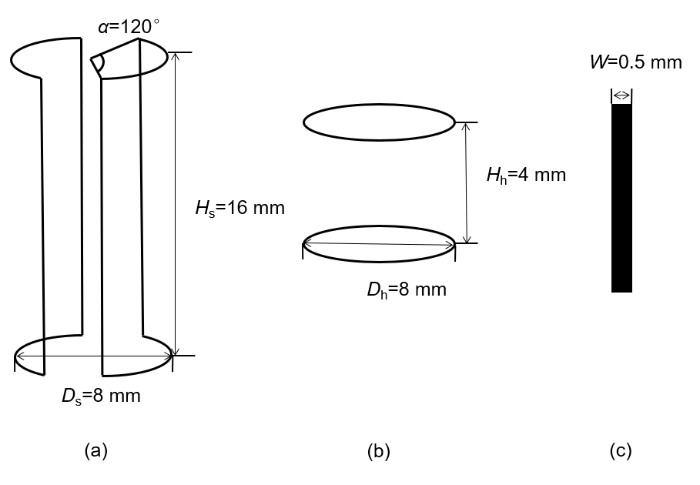
根据样品管尺寸，设定感兴趣区域为直径为5 mm，高度为4 mm的圆柱体.如图4所示，对于鞍形线圈，理论上高度Hs与直径Ds比值为2 : 1，且线圈角度α为120˚时，能够产生最为均匀的磁场[7]；而对于亥姆霍兹线圈，理论上其高度Hh是直径Dh的一半时，能够产生最为均匀的磁场[8].同时考虑线圈支架尺寸，设置鞍形线圈直径为8 mm，高度为16 mm；亥姆霍兹线圈直径为8 mm，高度为4 mm.由于线圈尺寸小，制作难度大，本设计采用柔性电路板印刷（FPC）的方式进行线圈设计.对应的导线仿真模型为矩形铜带.考虑到线圈要进行多匝的设计，线圈宽度设计为0.5 mm.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   (a)鞍形线圈尺寸示意图，线圈高度Hs为16 mm，线圈直径Ds为8 mm，线圈角度为120˚；(b)亥姆霍兹线圈尺寸示意图，线圈高度Hh为4 mm，线圈半径Dh为8 mm；(c)铜带宽度示意图，宽度W为0.5 mm

Fig. 4   (a) Schematic diagram of the saddle coil dimensions, with a coil height Hs of 16 mm, a coil diameter Ds of 8 mm, and a coil angle of 120˚; (b) Schematic diagram of the Helmholtz coil dimensions, with a coil height Hh of 4 mm and a coil radius Dh of 8 mm; (c) Schematic diagram of the copper strip width, with a width W of 0.5 mm


1.3 多匝线圈优化仿真

圆极化线圈的性能由其产生的射频场不均匀度δ 和信噪比SNRc决定，射频场不均匀度δ 计算公式为：

$\delta =\frac{{{B}_{\max }}-{{B}_{\min }}}{{{B}_{\text{mean}}}}\times 100 \%$

其中，${{B}_{\max }}$和${{B}_{\min }}$为射频场的磁感应强度最大值与最小值，${{B}_{\text{mean}}}$为感兴趣区域内射频场的磁感应强度的平均值，单位为T.

线圈相对信噪比SNRc计算公式为[3]：

$\text{SN}{{\text{R}}_{\text{c}}}=\frac{{{B}_{\text{mean}}}}{I\sqrt{R}}$

其中，I为通入线圈的激励电流，单位为A；R为线圈的交流电阻，单位为Ω.

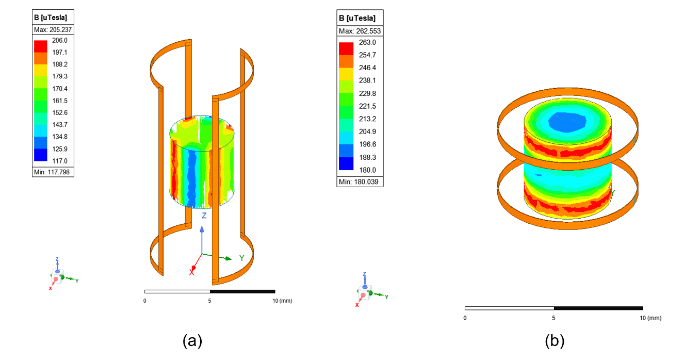
使用Ansys Maxwell仿真软件对鞍形线圈和亥姆霍兹线圈进行建模分析，激励电流强度为1 A，频率为22.5 MHz.图5显示了两种线圈在感兴趣区域内的磁场分布.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   (a)鞍形线圈与(b)亥姆霍兹线圈仿真. 圆柱体内颜色由蓝到红表示磁感应强度（μT）由弱到强. 鞍形线圈磁场沿y方向，亥姆霍兹线圈磁场沿z方向

Fig. 5   (a) Simulation of the saddle coil and (b) Helmholtz coil. The color gradient from blue to red within the cylinder represents the magnetic flux density (μT) increasing from weak to strong. The magnetic field direction of the saddle coil is along the y-axis, while that of the Helmholtz coil is along the z-axis


根据Ansys Maxwell仿真软件可以得到感兴趣区域内射频场的磁感应强度最大值${{B}_{\max }}$与最小值${{B}_{\min }}$，感兴趣区域内射频场的磁感应强度的平均值${{B}_{\text{mean}}}$和线圈的交流电阻R.从而可以计算出射频场不均匀度δ和线圈相对信噪比SNRc.

定义线圈的综合性能FoM (Figure of Merics)为线圈相对信噪比SNRc除以射频场不均匀度δ，计算公式如(6)式所示.

$\text{FoM}=\frac{\text{SN}{{\text{R}}_{\text{c}}}}{\delta }$

其中，相对信噪比与线圈性能成正比，故放在分子上；射频场不均匀度与线圈性能成反比，故放在分母上.由于空间尺寸的限制，鞍形线圈匝数最多为4匝，亥姆霍兹线圈匝数最多为6匝.分别对两组线圈的匝数进行仿真优化.仿真结果由表1和表2所示.从表1中可以获知，当鞍形线圈匝数为2时，其综合性能FoM最大；从表2中可以获知，当亥姆霍兹线圈匝数为5时，其综合性能FoM最大.此优化结果用于制造圆极化线圈实物.

表1   鞍形线圈综合性能

Table 1  Saddle coil comprehensive performance

线圈匝数归一化线圈相对信噪比SNRc射频场不均匀度δ综合性能FoM
15.37×10-40.560.96×10-3
27.25×10-40.631.14×10-3
38.16×10-40.791.03×10-3
48.36×10-40.970.86×10-3

新窗口打开| 下载CSV


表2   亥姆霍兹线圈综合性能

Table 2  Helmholtz coil comprehensive performance

线圈匝数归一化线圈相对信噪比SNRc射频场不均匀度δ综合性能FoM
24.92×10-40.766.46×10-4
35.56×10-40.678.30×10-4
45.90×10-40.708.37×10-4
56.03×10-40.728.41×10-4
66.08×10-40.738.28×10-4

新窗口打开| 下载CSV


2 圆极化线圈实物制作及测试

2.1 线圈实物制作

实际线圈采用FPC的工艺，利用嘉立创EDA软件进行设计制作.除了线圈，圆极化探头还包含线圈支架和调谐匹配电路.线圈支架用于固定线圈，使其能够稳定在特定区域内进行信号的激发与接收.调谐匹配电路是NMR探头的核心组件，主要用于调谐和匹配.调谐确保电路谐振频率与NMR频率一致，确保射频能量高效传输到样品，并接收样品产生的NMR信号.匹配则使电路阻抗与传输线阻抗匹配，从而最大化射频能量的传输效率并减少反射损耗.

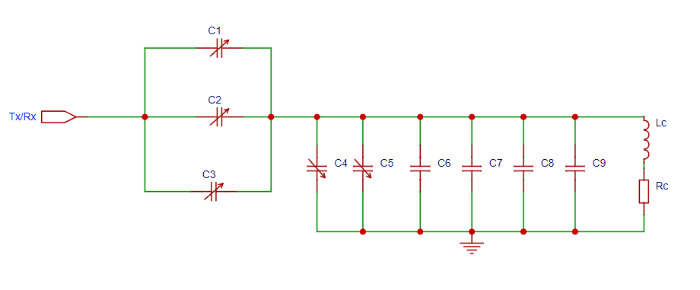
采用L型调谐匹配网络，如图6所示，L型网络是最简单，能够采用最低成本满足系统要求的匹配网络.其中，Tx/Rx代表发射与接收端口，Lc和Rc是线圈的等效电感与等效电阻，电容C1~C3用于调谐，电容C4~C9用于匹配.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   L型匹配网络，其中Lc与Rc是线圈等效电感与等效电阻，C1~C3为调谐电容，C4~C9为匹配电容

Fig. 6   L-type matching network, where Lc and Rc represent the equivalent inductance and equivalent resistance of the coil, respectively, C1~C3 is the tuning capacitor, and C4~C9 is the matching capacitor


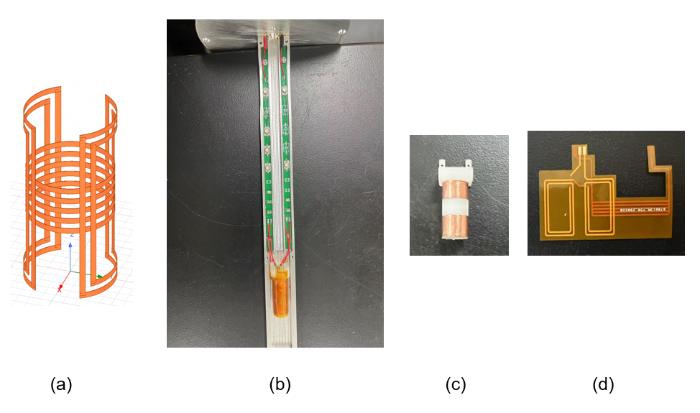
参照第1节中最优鞍形线圈与亥姆霍兹线圈参数，在嘉立创EDA中设计好FPC平面线圈结构，FPC顶层为鞍型线圈结构，底层为亥姆霍兹线圈结构，将其均匀贴合并使用高温绝缘胶带固定在3D打印的线圈支架上，由于感兴趣区域为4 mm高圆柱体，鞍形线圈高度为16 mm，为了避免鞍形线圈激发感兴趣区域外的样品，使用7 mm宽的铜胶带分别贴合在支架圆柱体上下两端.使用漆包线将线圈连接到调谐匹配电路板，并将线圈和调谐匹配电路安装在设计好的屏蔽铝壳内.两个通道线圈的磁场方向相互正交实现空间上的解耦.探头及线圈3D模型和实物如图7所示，由于实际制作的FPC线圈需要考虑馈电端口，实际线圈的构型与理论仿真模型有一定的出入.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   (a)优化参数后圆极化线圈三维示意图；(b)探头实物图；(c)线圈支架实物图；(d)线圈实物图

Fig. 7   (a) 3D schematic diagram of the circularly polarized coil after parameter optimization; (b) Physical image of the probe; (c) Physical image of the coil holder; (d) Physical image of the coil


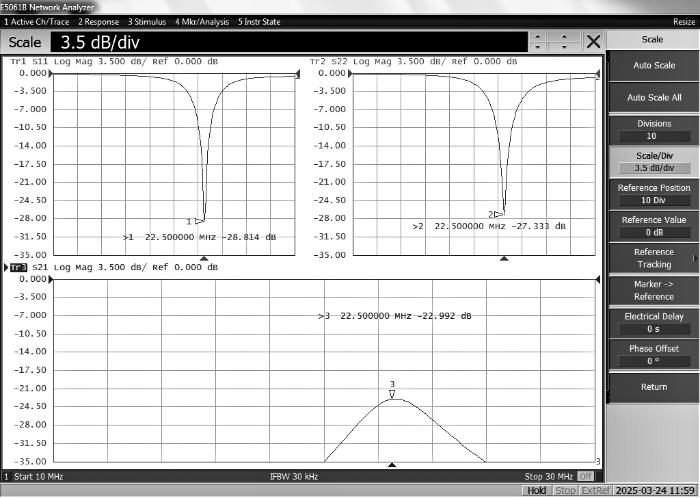
选用氢核为样品信号检测核，调节调谐匹配电路板上的电容使线圈谐振在0.53 T下氢核的拉莫尔频率（22.5 MHz）.使用Keysight公司的E5061B矢量网络分析仪测量了两线圈在22.5 MHz的回波损耗参数S11以及隔离度参数S21.S11和S22分别反映探头与射频源及样品之间的阻抗匹配情况，低值表示能量传输效率高；S21则衡量探头的隔离性能，低值表明信号串扰小[9].结果如图8所示，其中横坐标为频率，从10 MHz到30 MHz，纵坐标为S11参数.鞍形和亥姆霍兹线圈在22.5 MHz频率下的S11和S22分别为-28.814 dB和-27.333 dB，隔离度S21为-22.992 dB.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   鞍形与亥姆霍兹线圈的S参数测量结果. 左上角1号标签表示鞍形线圈在22.5 MHz频率下S11 = -28.814 dB；右上角曲线2号标签表示亥姆霍兹线圈在22.5 MHz频率下S22 = -27.333 dB；下方图像中的3号标签表示两线圈在22.5 MHz频率下间的隔离度为S21 = -22.992 dB

Fig. 8   Measurement results of the S-parameters for the Helmholtz and saddle coils. The label "1" in the upper left corner indicates that the curve corresponds to the saddle-type coil, showing S11 = −28.814 dB at 22.5 MHz. The label "2" in the upper right corner represents the Helmholtz coil, with S22 = −27.333 dB at the same frequency (22.5 MHz). The lower curve labeled "3" indicates the inter-coil isolation at 22.5 MHz, with an S21 parameter of −22.992 dB


2.2 Hybrid电桥制作

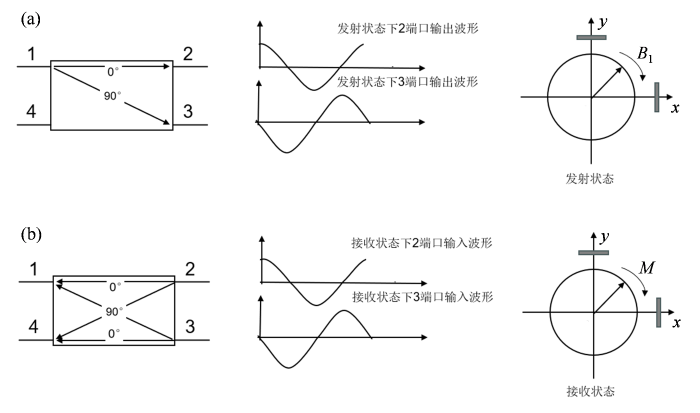
探头产生圆极化的场需要有两个馈电端口，且两端口具有相等振幅和90˚相位差的源激励.如图9所示，Hybrid电桥由4个端口构成，1端口接入射频功放，2端口和3端口接入x、y两个独立的线圈，4端口接入Rx接收端.在发射状态下，端口4与端口1隔离.脉冲功率以正交模式分配到端口2和端口3，从而产生旋转圆极化磁场[10,11]；接收状态下，旋转磁化在x线圈和y线圈中感应出电压相位差为90˚的信号.它们被输入到混合器的2端口和3端口，2端口和3端口彼此隔离.1端口和4端口的信号相位发生偏移，在4端口同相出现的两个正交信号被相加，而在1端口则反相出现，从而相互抵消，确保没有信号泄漏到发射负载.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   Hybrid电桥信号原理框图. (a)发射状态下信号流程；(b)接收状态下信号流程

Fig. 9   Hybrid bridge signal principle diagram. (a) Signal flow in the transmission state; (b) Signal flow in the reception state


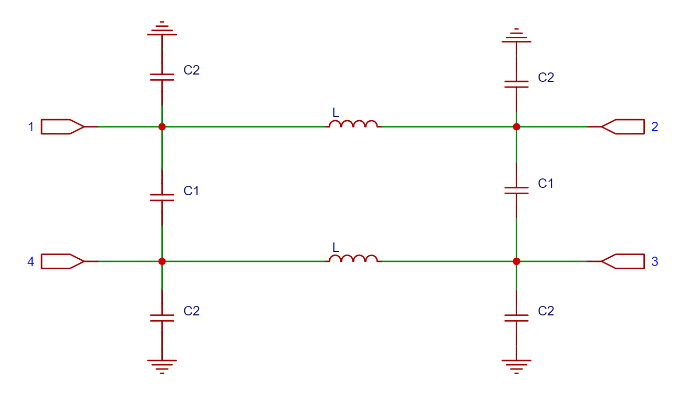
实际采用集总参数元件制作Hybrid电桥电路，基于λ/8传输线[12]，设计出适合于22.5 MHz频率下的电路，图10为Hybrid集总参数电路图.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   等效于λ/8的集总元件电路Hybrid电桥

Fig. 10   Lumped element circuit equivalent to the λ/8 quad hybrid


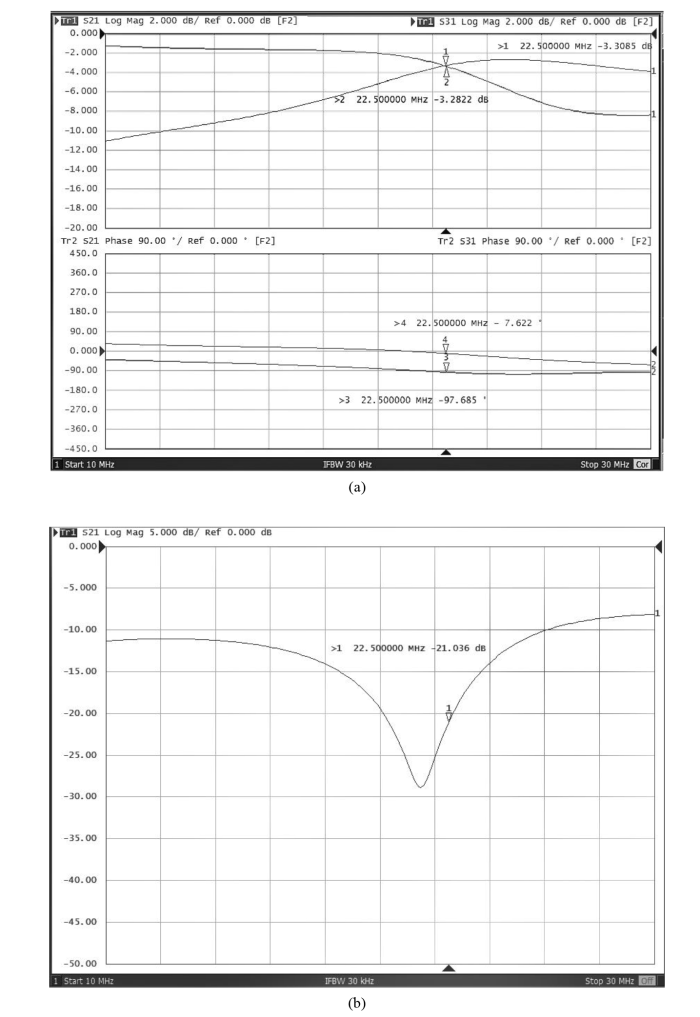
图11为实际调试的Hybrid电桥参数.其中(a)中1号标签与2号标签分别表示2端口、3端口与1端口插入损耗，在22.5 MHz下S21为-3.309 dB和-3.282 dB；(a)中3号标签与4号标签分别表示2端口、3端口与1端口相移度数，在22.5 MHz下分别为-97.685˚和-7.622˚，其相位差为-90.063˚.(b)中曲线S21为2端口和3端口隔离度，1号标签标表示在22.5 MHz下S21为-21.036 dB，说明2端口与3端口隔离度较好.证明在发射状态下，此Hybrid电桥可以实现1端口激励，2端口与3端口产生等幅且相差为90˚的信号；由于电路为对称结构，在接收状态下，S12与S21相等[13]，且两者相位差也相等；S13与S31相等，两者相位差也相等.故此电路可用于圆极化探头中.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   Hybrid电桥S参数. (a) 2端口，3端口与1端口插入损耗与相移；(b) 2端口与3端口隔离度

Fig. 11   S-parameters of the hybrid bridge. (a) Insertion loss and phase shift for Port 2, Port 3, and Port 1; (b) Isolation between Port 2 and Port 3


2.3 圆极化线圈性能测试

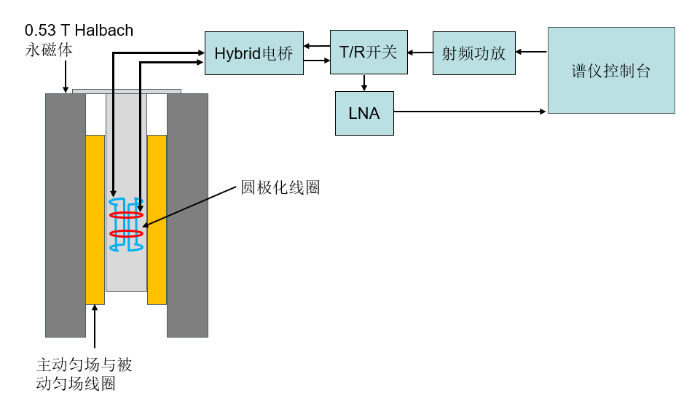
在实验室的桌面磁共振平台上进行圆极化探头性能测试：磁体选用在5 mm球状区域内均匀度为3 ppm（1 ppm = 1×10-6）的自研0.53 T Halbach永磁体[14,15]，T/R开关，LNA和Hybrid电桥均为自研适用于22.5 MHz的射频组件[16].射频功率放大器采用美国Tecmag公司的BT00500-AlphaSA型号，谱仪采用Tecmag公司的Tecmag Scout LF1型号.各组件通过同轴线相互连接.测试系统框图如图12所示.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12   测试系统框图

Fig. 12   Block diagram of the testing system


使用90˚硬脉冲激发，通道的样品为6.4 g/L的CuSO4溶液（购自西安天茂宝鼎生物科技有限公司的分析纯CuSO4•5H2O溶解于去离子水配制而成），分别对单通道的鞍形线圈，单通道亥姆霍兹线圈，以及对组合后的最优圆极化线圈进行氢信号测试.单通道亥姆霍兹和鞍形线圈90˚硬脉冲的序列参数[17]为：脉宽为8 μs，频谱宽度为20 kHz，数据点数为4 096；正交线圈的90˚硬脉冲序列参数为：脉宽为5 μs，频谱宽度为20 kHz，数据点数为4 096.信噪比的计算依据是通过对信号的最大幅值与噪声水平的比值进行评估，其中信号的最大幅值直接从信号中提取，而噪声水平则通过信号的统计特性来估计，基于信号的方差和差分乘积，确保能够准确反映噪声的水平.定义信噪比SNR的计算公式如下：

$\text{SNR}=\frac{\text{maxval}}{2*\text{noise}}$

其中maxval是信号范围内的信号最大值，noise计算方法如(8)式所示：

$\text{noise}=\sqrt{\frac{\sum\nolimits_{i=-n}^{n}{y}{{(i)}^{2}}-\frac{1}{N}{{\left( \sum\nolimits_{i=-n}^{n}{y}(i) \right)}^{2}}+\frac{3\cdot {{\left( \sum\nolimits_{i=1}^{n}{i\cdot (y}(i)-y(-i)) \right)}^{2}}}{{{N}^{2}}-1}}{N-1}}$

其中N为信号范围内的总采样点数，n为(N-1)/2，y(i)为信号区间范围内的第i点的强度值.

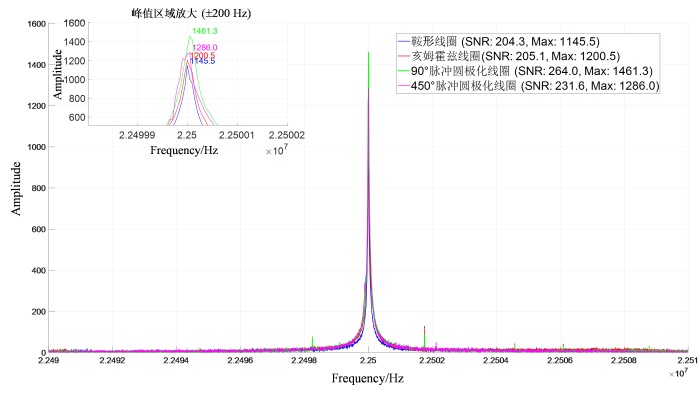
进行10次重复实验对信号进行采集，取最优的一组信号进行展示，测得单通道线圈与圆极化线圈最优的谱图如图13所示.图13中蓝色曲线为单通道的鞍形线圈测得氢谱图信号最佳信噪比SNR为204.32，红色曲线为单通道的亥姆霍兹线圈测得氢谱图信号信噪比最佳SNR为205.01，绿色曲线为组合后的最优圆极化线圈测得氢谱图信号最佳信噪比为264.01. 由此可知，本文设计的圆极化线圈相较于单通道亥姆霍兹线圈和单通道的鞍形线圈，信噪比分别提升了28.78%和29.21%.图13中粉色曲线为450˚翻转角下信号谱图，强度约为1 286，与90˚翻转角下信号强度1 461的比值约为88%，一般要求比值大于85%则认为B1场较均匀，说明本设计的圆极化线圈射频场均匀度较好[18].由序列信息可知，单通道的硬脉冲长度为8 μs，圆极化探头的硬脉冲长度为5 μs，在脉冲功率幅值不变的前提下，可以简单把发射功率与脉冲时间长度看作正比关系，所以相比较于单通道的线圈，圆极化的发射功率大约减小了37.5%.本设计的圆极化探头在理论上并未实现增加$\sqrt{2}$倍信噪比的提升和节省一半功率的效果，原因可能有如下几点：（1）线圈损耗，由于线圈导体电阻会额外消耗能量，且高频下趋肤效应加剧了导体电阻[19]，故线圈在发射和接收状态下均存在能量损耗；（2）制作误差，由于正交线圈是二维的平面柔性印刷电路板（FPCB）绕制为三维的结构，存在线圈结构的偏差，可能导致实际产生的并非标准的圆极化场，而是椭圆极化，导致线圈在发射和接收状态下存在能量损耗.

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13   单通道线圈与圆极化线圈测得的1H NMR谱图. 蓝色曲线为单通道90˚脉冲鞍形线圈测得1H NMR信号；红色曲线为单通道90˚脉冲亥姆霍兹线圈测得1H NMR信号；绿色和粉色曲线分别为圆极化线圈90˚和450˚脉冲测得1H NMR信号

Fig. 13   The figure compares 1H NMR spectra acquired using different coil configurations. The blue curve represents the 1H NMR signal measured with a single-channel saddle coil using a 90˚ pulse. The red curve shows 1H NMR data obtained from a single-channel Helmholtz coil with identical 90˚ pulse excitation. In contrast, the green and magenta curves display 1H NMR signals acquired with circularly polarized (CP) coils employing 90˚ and 450˚ pulse excitations respectively


3 结论

本文设计了一套应用于桌面磁共振波谱仪的圆极化射频探头，该线圈由鞍形和亥姆霍兹线圈组成.使用有限元仿真软件Ansys Maxwell对线圈匝数进行仿真性能对比，得到最优匝数，并制作实物.配合外围的Hybrid电桥，T/R开关、LNA和谱仪系统完成信号测试.结果表明，两线圈之间串扰小.圆极化线圈的谱图信噪比相较于单通道线圈最大提升了29.21%，发射功率减小了约37.5%.验证了本文设计的圆极化探头在桌面级磁共振波谱仪的可行性.

利益冲突

无

参考文献

RULE G S, HITCHENS T K. NMR spectroscopy[M]. Springer, 2006.

[本文引用: 1]

WANG Y, XU Y, WANG F, et al.

A passive shimming method for Halbach magnet based on magnetic sheet arrays

[J]. J Magn Reson, 2022, 339: 107210.

[本文引用: 1]

WANG F, LIU T W, XU Y J, et al.

Design of a miniaturized nuclear magnetic resonance radio frequency probe with an external lock channel

[J]. Chinese J Magn Reson, 2023, 40(3): 332-340.

[本文引用: 2]

王峰, 刘庭伟, 徐雅洁, 等.

一种带外部锁场通道的小型化核磁共振射频探头设计

[J]. 波谱学杂志, 2023, 40(3): 332-340.

DOI:10.11938/cjmr20223044      [本文引用: 2]

温度漂移是影响桌面式核磁共振波谱仪测量精度的一个重要因素，在探头中添加锁场线圈实现场频联锁是抑制温度漂移的常用手段．本文基于实验室紧凑型Halbach磁体，设计了一套带有外部锁场功能的双通道探头．针对目标区域，使用COMSOL仿真对比了螺线管线圈、鞍形线圈和亥姆霍兹线圈的磁场均匀性、信噪比和品质因数，发现螺线管线圈具有最佳综合性能．进一步针对螺线管线圈结构，对线圈直径、高度、匝数、匝间距以及漆包线半径进行了仿真优化，得到漆包线半径为0.4 mm、线圈直径和高度为8.2 mm、匝间距为1.6 mm、匝数为5是最优螺线管尺寸．基于仿真结果，制作了探头实物，并配合外围电路进行测试．结果表明，两个线圈通道之间串扰较小，信号检测通道信噪比达到50以上，锁场通道信噪比达到20以上．锁场实验结果表明，添加锁场后整体系统的频率漂移约为0.2 ppm/h（1 ppm=10<sup>-6</sup>），验证了此探头设计可用于基于紧凑型Halbach磁体的磁共振设备．

WAN C, HE W, SHEN S, et al.

Design of an orthogonal receive coil for ultra-low field magnetic resonance imaging of the knee joint

[J]. Transactions of Electrotechnical Society, 2024, 39(7): 1923-1931.

[本文引用: 1]

万裁, 何为, 沈晟, 等.

超低场磁共振膝关节正交接收线圈设计

[J]. 电工技术学报, 2024, 39(7): 1923-1931.

[本文引用: 1]

DING M X, CHU Y S, BAO S H.

Design of a radio frequency broadband circularly polarized tuning probe

[J]. J Electr Eng Technol, 1997, (1): 15-17.

[本文引用: 3]

丁美新, 储岳森, 鲍胜浩.

射频宽带圆极化调谐探头的设计

[J]. 电工技术杂志, 1997, (1): 15-17.

[本文引用: 3]

CHEN C N, HOULT D I, SANK V J.

Quadrature detection coils—A further $\sqrt{2}$ improvement in sensitivity

[J]. J Magn Reson, 1983, 54(2): 324-327.

[本文引用: 1]

GINSBERG D M, MELCHNER M J.

Optimum geometry of saddle shaped coils for generating a uniform magnetic field

[J]. Rev Sci Instrum, 1970, 41(1): 122-123.

[本文引用: 1]

TROUT S R.

Use of Helmholtz coils for magnetic measurements

[J]. IEEE Trans Magn, 1988, 24(4): 2108-2111.

[本文引用: 1]

LEE R F, GIAQUINTO R O, HARDY C J.

Coupling and decoupling theory and its application to the MRI phased array

[J]. Magn Reson Med, 2002, 48(1): 203-213.

PMID:12111947      [本文引用: 1]

In classical MRI phased-array design, optimal coil overlapping is used to minimize coupling between nearest-neighbor coils, and low input impedance preamplifiers are used to isolate the relatively weak coupling between non-nearest neighbors. However, to make the complex sensitivities of phased-array coils sufficiently distinct in parallel spatially-encoded MRI, it is desirable to have no overlapping between coils. Also, if phased arrays are used as transmit coils in MRI, one can no longer rely on the low input impedance of the preamplifiers for decoupling. Here a coupling and decoupling theory is introduced to provide a better understanding of the relations between coupled and uncoupled signals in the MRI phased array, and to offer a new method for decoupling phased-array coils without overlapping the nearest coil pairs. The new decoupling method is based on the assumption that any n-element phased array can be decoupled by a 2n-port interface system between phased array and preamplifiers. The detailed analysis and the experimental results show that a four-port interface can be used to decouple a two-element phased array. Furthermore, the four-port interfaces can serve as building blocks to construct a 2n-port decoupling interface. This new method allows one to place the coil elements anywhere that could optimize parallel spatial encoding without concern for coupling between the coils. The method can also be used for phased-array transmit coils.Copyright 2002 Wiley-Liss, Inc.

TOMANEK B, VOLOTOVSKYY V, TYSON R, et al.

A quadrature volume RF coil for vertical B0 field open MRI systems

[J]. Concepts Magn Reson Part B Magn Reson Eng, 2016, 46(3): 118-122.

[本文引用: 1]

GIOVANNETTI G, FRIJIA F, FLORI A, et al.

Design and simulation of a Helmholtz coil for magnetic resonance imaging and spectroscopy experiments with a 3T MR clinical scanner

[J]. Appl Magn Reson, 2019, 50(9): 1083-1097.

[本文引用: 1]

KANG K, XU Y J, ZHANG W W, et al.

Research and design of a low-noise preamplifier for low-field magnetic resonance systems

[J]. Chinese J Magn Reson, 2017, 34(3): 383-395.

[本文引用: 1]

亢科, 徐雅洁, 张闻文, 等.

低场磁共振系统的低噪声前置放大器研究设计

[J]. 波谱学杂志, 2017, 34(3): 383-395.

DOI:10.11938/cjmr20162547      [本文引用: 1]

噪声前置放大器是磁共振射频接收子系统中的重要组件，它的性能优劣直接决定了最终磁共振图像的好坏.目前市场上的低噪声前置放大器大多基于中高场磁共振系统开发，而针对低场磁共振系统的很少；另外，商用低场磁共振系统的低噪声前置放大器价格相对较贵，并且多采用两级放大结构，结构复杂、调试难度大、成本相对较高.在此背景下，针对0.5 T低场磁共振设备利用Keysight公司的先进设计系统（ADS）软件对低噪声前置放大器进行研究设计，采用一级放大结构，探索电路设计与布局对放大器性能的影响.实测结果表明自主设计的低噪声前置放大器在21 MHz共振频率附近噪声系数为0.5 dB左右，增益达到了30 dB，能够满足低场磁共振应用的要求.

GRUBER B, FROELING M, LEINER T, et al.

RF coils: A practical guide for nonphysicists

[J]. J Magn Reson Imaging, 2018, 48(3): 590-604.

[本文引用: 1]

CHEN Q, XU Y, CHANG Y, et al.

Design and demonstration of four-channel received coil arrays for vertical-field MRI

[J]. Appl Magn Reson, 2017, 48: 501-515.

[本文引用: 1]

XU Y, WANG F, WANG Y, et al.

Active shim coils design for Halbach magnet based on inverse boundary element method

[J]. Magn Reson Lett, 2022, 2(3): 159-169.

[本文引用: 1]

WU B, QU P, WANG C, et al.

Interconnecting L/C components for decoupling and its application to low-field open MRI array

[J]. Concepts Magn Reson Part B Magn Reson Eng, 2007, 31(2): 116-126.

[本文引用: 1]

XU Y, YU P, JIA F, et al.

A spherical harmonics decomposition method (SHDM) for irregular matrix coils design

[J]. IEEE Trans Biomed Eng, 2021, 69(4): 1292-1301.

[本文引用: 1]

MILLER J B, SUITS B H, GARROWAY A N.

Circularly polarized RF magnetic fields for spin-1 NQR

[J]. J Magn Reson, 2001, 151(2): 228-234.

[本文引用: 1]

MISPELTER J, LUPU M, BRIGUET A. NMR probeheads for biophysical and biomedical experiments: theoretical principles and practical guidelines[M]. World Scientific Publishing Company, 2015.

[本文引用: 1]

/

〈 〉

网站设计版权所有 © 2017 《波谱学杂志》编辑部
地址：湖北省武汉市武昌区小洪山西30号 中科院精密测量科学与技术创新研究院波谱楼 《波谱学杂志》编辑部
邮编：430071　电话/传真：(086)027－87198791   E-mail: magres@wipm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发